Предмет: Алгебра,
автор: n408341
ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО НАДО
АЛГЕБРА 8 КЛАСС
Приложения:
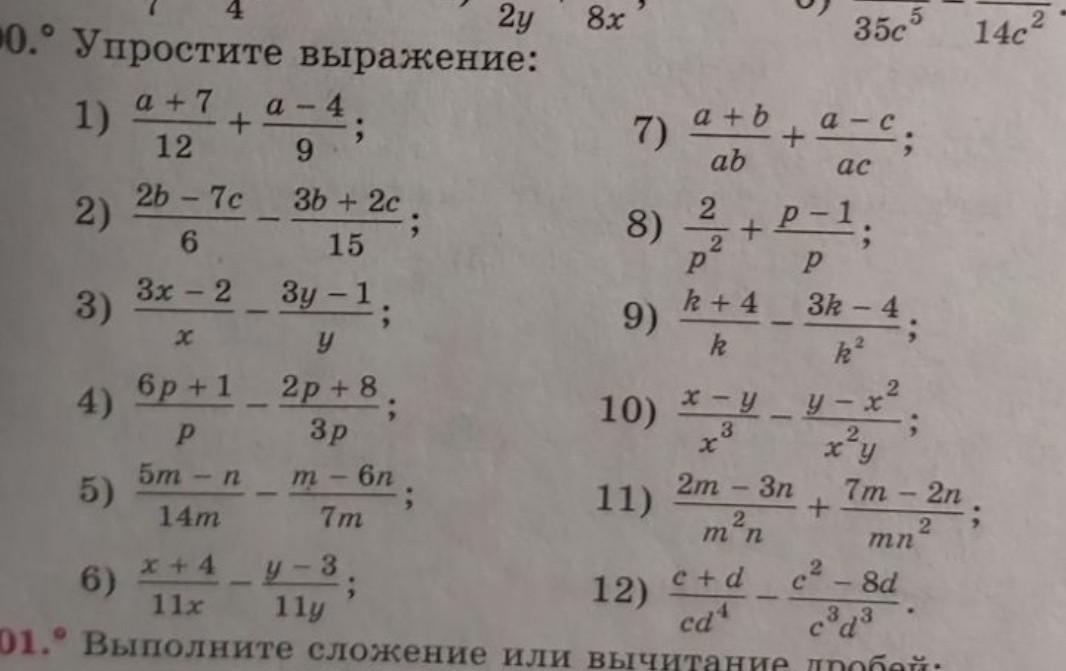
Ответы
Автор ответа:
1
Ответ:
Объяснение:
1) +
=
=
=
2) -
=
=
=
3)-
=
=
=
4) -
=
=
=
5)-
=
=
=
6) -
=
=
=
7) +
=
=
=
=
8) +
=
9) -
=
=
=
10) -
=
=
=
11) +
=
=
=
=
12) -
=
=
=
Похожие вопросы
Предмет: Українська література,
автор: vikaostafijcuk75
Предмет: Українська мова,
автор: mamalita1234d
Предмет: Математика,
автор: viktoriaklimec854
Предмет: Алгебра,
автор: Аноним
Предмет: Русский язык,
автор: seazpubgm