Question

Очень срочно умоляяяяяяю
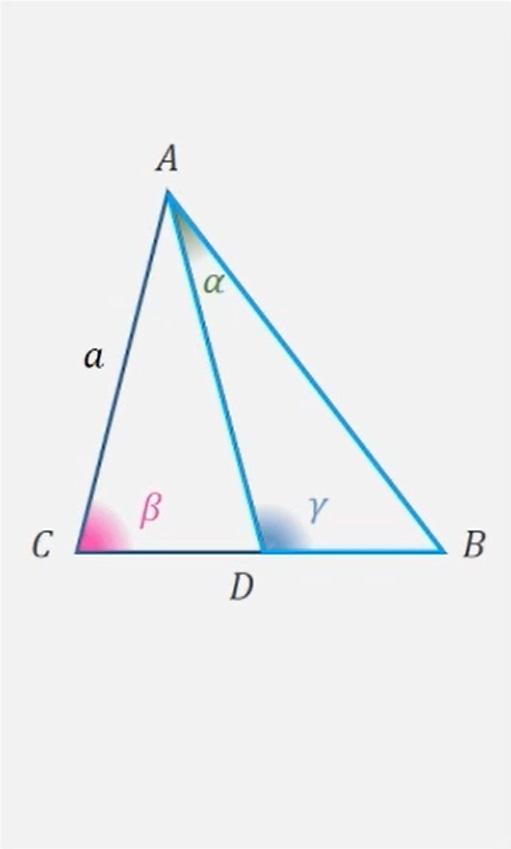
Точка D обозначена на стороне BC треугольника ABC.

AC = a

∠ADB = γ,

∠ACB = β,

∠BAD = α.

Найдите BD.

Прошу, пожалуйста, максимально подробно. Я знаю ответ, мне важно решение. Я не понимаю!

Answer 1

Ответ:

$\displaystyle BD=\frac{a\;sin\beta \;sin\alpha }{sin\gamma\;sin(\alpha +\gamma)}$

Объяснение:

Точка D обозначена на стороне BC треугольника ABC.

AC = a; ∠ADB = γ, ∠ACB = β, ∠BAD = α.  Найдите BD.

Дано: ΔАВС;

D ∈ BC;

AC = a; ∠ADB = γ, ∠ACB = β, ∠BAD = α.

Найти: BD

Решение:

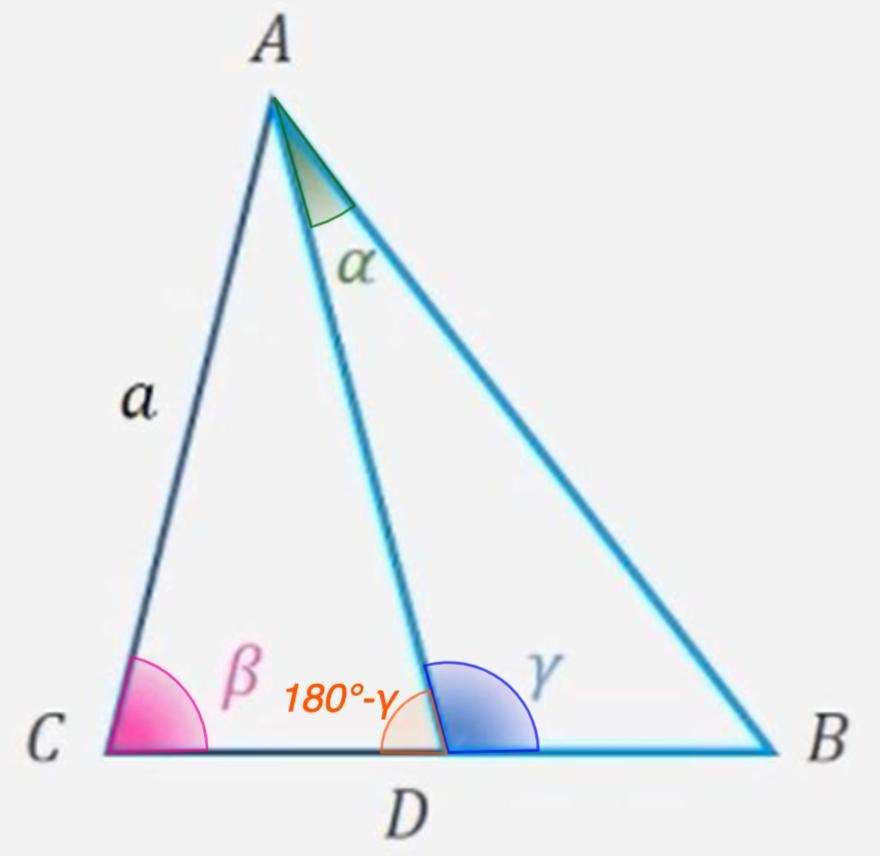
1. Рассмотрим ΔСAD.

• Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов.

$\displaystyle \frac{AD}{sin\beta } =\frac{AC}{sin\angle CDA}$

• Сумма смежных углов равна 180°.

⇒ ∠CDA = 180° - γ

• Формула приведения:

    sin(180°-α) = sinα

$\displaystyle \frac{AD}{sin\beta } =\frac{a}{sin\gamma}\\\\AD=\frac{a\;sin\beta }{sin\gamma}$

2. Рассмотрим ΔDAB.

По теореме синусов:

$\displaystyle \frac{AD}{sin\angle B } =\frac{DB}{sin\alpha }$

• Сумма углов треугольника равна 180°.

⇒ ∠B = 180° - (α + γ)

По формуле приведения:

sin∠B = sin(180° - (α + γ)) = sin (α + γ)

$\displaystyle \frac{a\;sin\beta }{sin\gamma\;sin(\alpha +\gamma) } =\frac{BD}{sin\alpha }\\\\ \bf BD=\frac{a\;sin\beta \;sin\alpha }{sin\gamma\;sin(\alpha +\gamma)}$