Предмет: Геометрия,
автор: valeri777ua
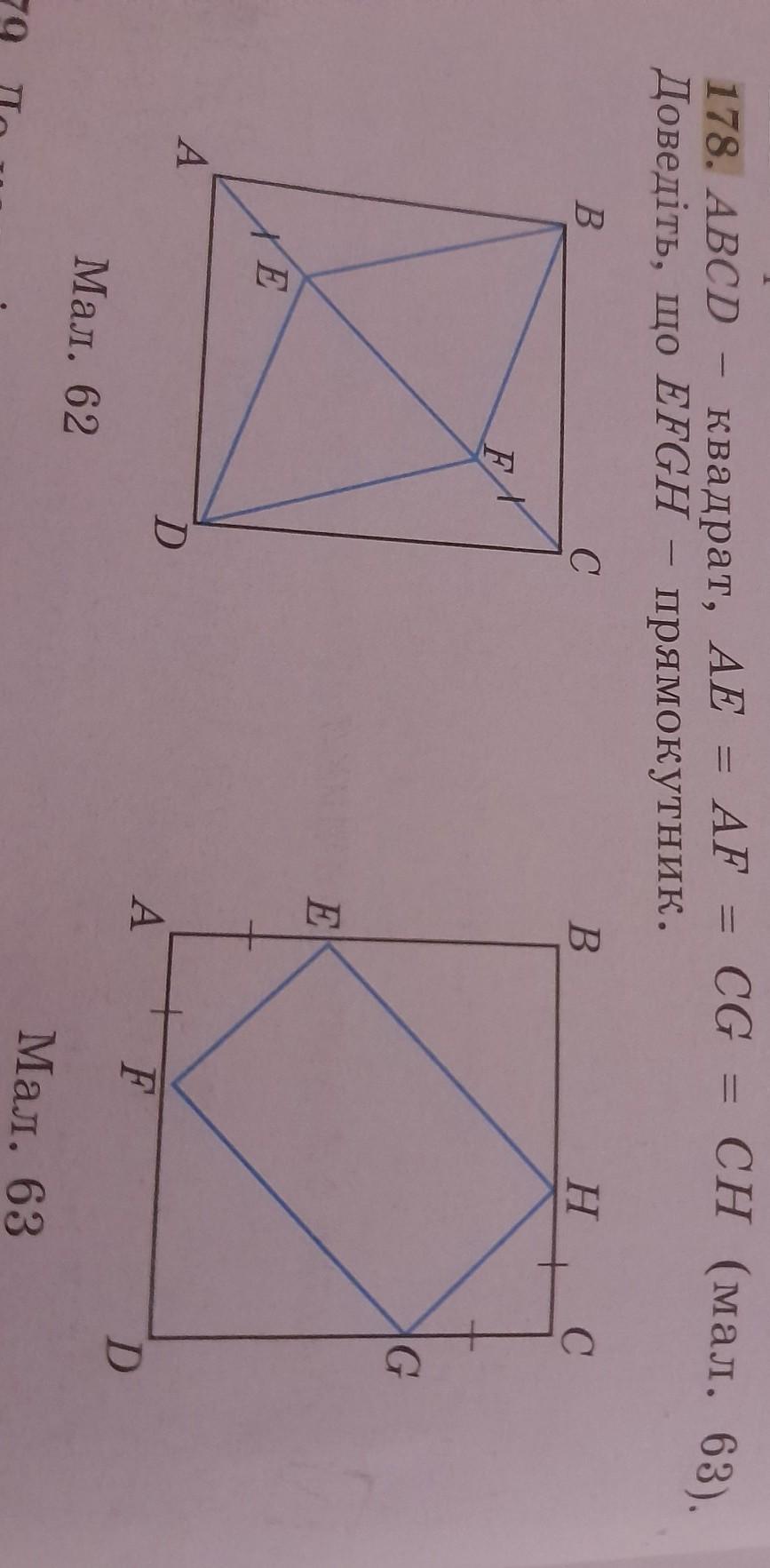
ABCD— квадрат, AE=AF=CG=CH (мал.63).
Доведіть, що EFGH—прямокунтник.
Приложения:
Ответы
Автор ответа:
3
Ответ:
Довели, що EFGH - прямокутник.
Объяснение:
ABCD — квадрат, AE = AF = CG = CH. Доведіть, що EFGH — прямокутник.
Доведення
1.
Розглянемо △AEF і △HCG.
- ∠A=∠C - як кути квадрата ABCD
- AE=AF=CG=CH - за умовою
△AEF = △HCG за двома катетами. Тоді EF = HG.
2.
Сторони квадрата рівні: AB=BC=CD=AD. AE=AF=CG=CH - за умовою. Якщо від рівних відрізків відняти рівні, то отриманні відрізки також будуть рівними: EB = BH = GD = DF.
Тому △EBH = △GDF за двома катетами, звідки EH = FG.
3.
- Чотирикутник є паралелограмом, якщо його протилежні сторони попарно рівні
EFGH — паралелограм (за ознакою).
4.
△EBH, △HCG, △EAF, △GDF — рівнобедрені прямокутні, отже, їх гострі кути дорівнюють по 45°.
5.
За аксиомою вимірювання кутів маємо:
∠AEF + ∠FEH + ∠HEB = 180°.
∠FEH = 180° - (∠AEF +∠HEB) = 180° - (45° + 45°) = 90°.
- Якщо один кут параллелограмма прямий, то такий паралелограм є прямокутником.
Отже, EFGH — прямокутник (за ознакою).
Довели.
#SPJ1
Похожие вопросы
Предмет: Химия,
автор: adelinahalykova
Предмет: Английский язык,
автор: viktoriakracevska
Предмет: Математика,
автор: maralbinoliyeva07
Предмет: Математика,
автор: Аноним