Предмет: Геометрия,
автор: violettak393
РЕШИТЕ ПОЖАЛУЙСТА, ТЕОРЕМА СИНУСОВ!!!
Приложения:
Ответы
Автор ответа:
0
Ответ:
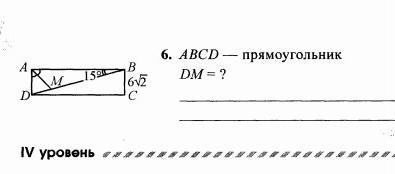
ABCD - прямоугольник ⇒ ∠А = 90° ,
АМ - биссектриса ⇒ ∠ВАМ =∠DAM = 45°
∠ABD = 15° ⇒ так как сумма углов в треугольнике = 180° , то в ΔАВМ : ∠АМВ = 180° - 45° - 15° =120°
Так как углы ∠АМВ и ∠АМD - смежные , то ∠АМD=180° - 120° = 60°
В прямоугольнике противоположные стороны равны, значит AD = BC = 6√2 .
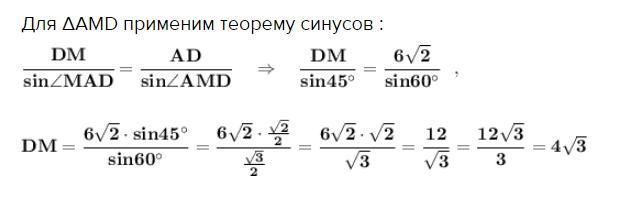
Для ΔАМD применим теорему синусов :
Приложения:
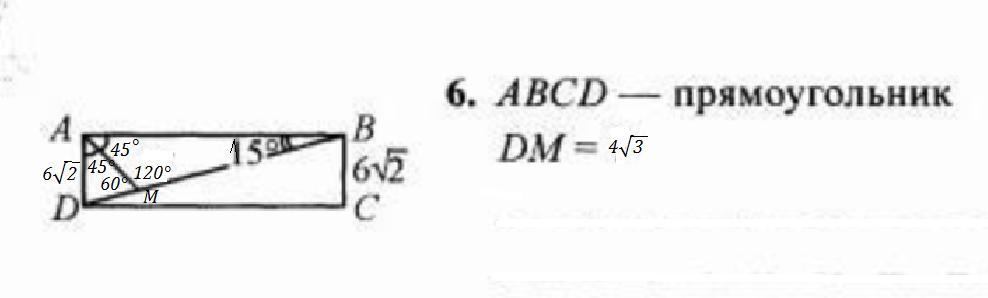
violettak393:
это неправильно, там должно быть 6 корней из 2
а, нет это другой вариант
все правильно
Похожие вопросы
Предмет: Литература,
автор: sploshnayaa
Предмет: Английский язык,
автор: veradrotenko0
Предмет: Українська література,
автор: vladiktropin
Предмет: Литература,
автор: HelpxMaryam
Предмет: Геометрия,
автор: ihiggcugihih