Question

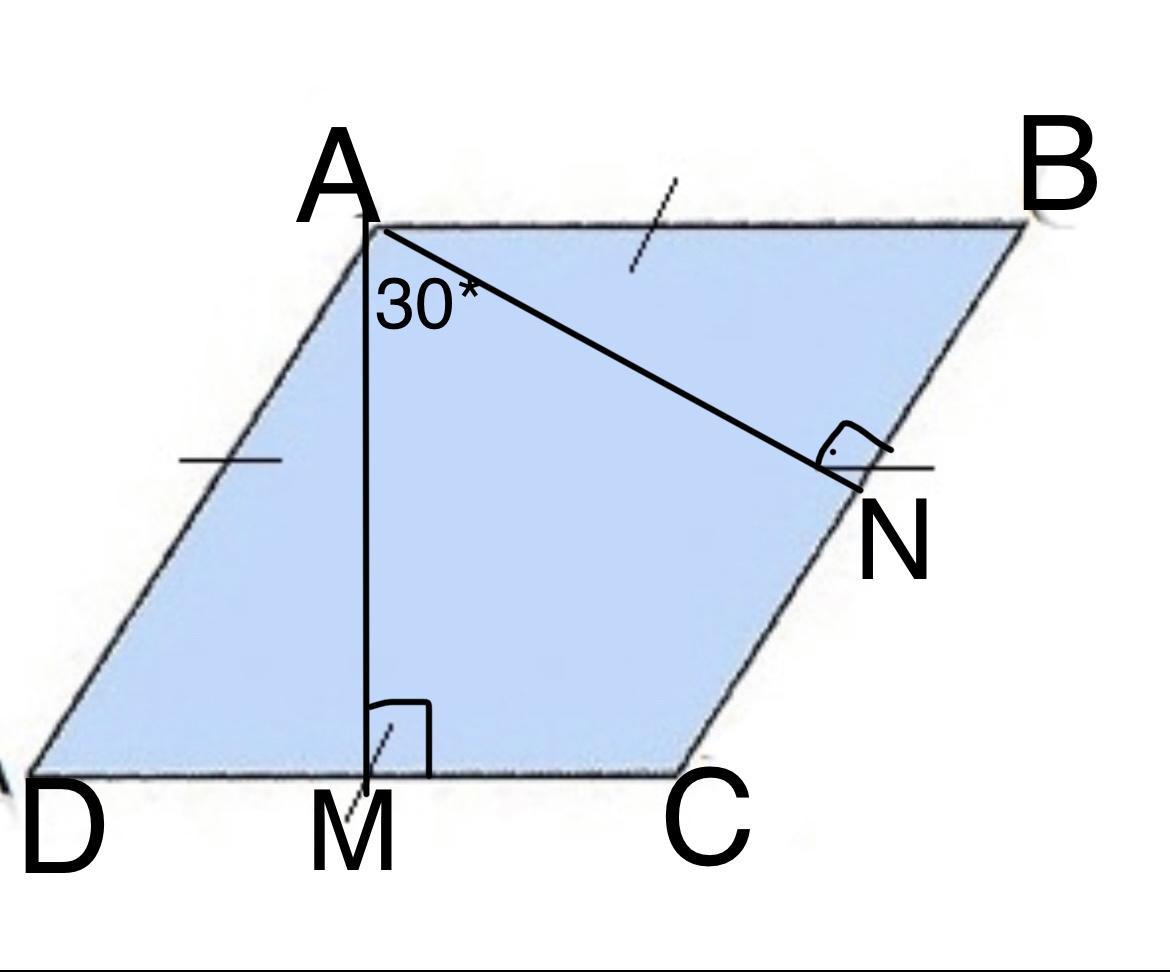
У ромбі ABCD з вершини тупого кута А проведено висоти AM і AN до сторін DC і ВС відповідно. Знайдіть
периметр ромба, якщо АМ = 9 дм, LMAN = 30°.

Answer 1

Відповідь:

72 дм.

Пояснення:

Дано: ABCD - ромб; ∠А - тупий кут; АМ ⊥ DC; AN ⊥ BC; AM = 9 дм; ∠МАN=30*.
Знайти:

Равсd - ?

Розв‘язання:

Сума кутів чотирикутника становить 360*.
У чотирикутнику МАNC:
∠С = 360 - ( ∠СМА + ∠МАN + ∠ANC);

∠C = 360- (90+30+90)= 360-210 = 150*

У ромба сума кутів, прилеглих до однієї сторони, становить 180*:

∠С + ∠D = 180

∠D = 180 - 150 = 30*.

У прямокутному трикутнику DAM (∠DMA=90*), ∠ADM = 30*.
Катет, що лежить напроти кута 30*, дорівнює половині гіпотенузи:

АМ = 1/2 • АD

AD = 2• AM

AD = 2•9 = 18 (дм)

Сторони ромба рівні.

Рabcd = 4•AD

P = 4•18 = 72 (дм).
Відповідь: 72 дм

Answer 2

Ответ:

76дм

Объяснение:

1) т.к. высота АМ- высота то, угол ДМА равен 90°

2) DC параллельно AB по свойству параллелограмма (ромб = параллелограмм). по свойству парасельных прямых и секущей между ними угол DMA=MAB.

3) L NAB= 90° - 30° = 60°

4) треугольник ABC прямоугольный. По свойству прямоугольного треугольника если угол равен 30° то противолежащий катет равен 1/2гипотенузы.

находим гипотенузу АВ=18

5) так как все стороны ромба равны то P ABCD=a×4=18×4=72дм.

Ответ: 72дм