Предмет: Алгебра,
автор: ysmina02
Доведіть тотожність рівняння.
Приложения:
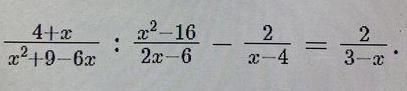
Ответы
Автор ответа:
1
Ответ:
Доказать тождество
.
Упростим выражение , стоящее в левой части равенства . Применяем формулу разности квадратов и квадрата разности .
Приложения:
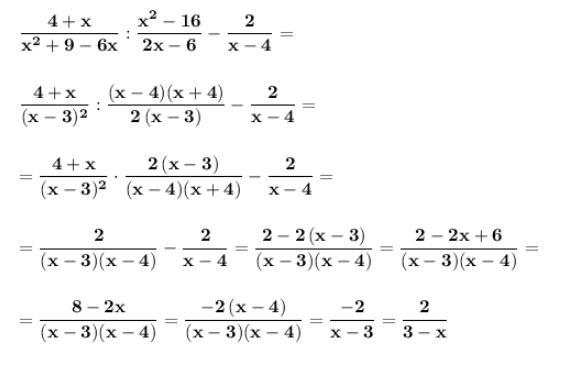
ysmina02:
Дякую
Похожие вопросы
Предмет: Английский язык,
автор: dindar12
Предмет: Українська мова,
автор: revenkoartem225
Предмет: Українська мова,
автор: diana121393
Предмет: Алгебра,
автор: 098765bah
Предмет: Математика,
автор: tronikevgenia200