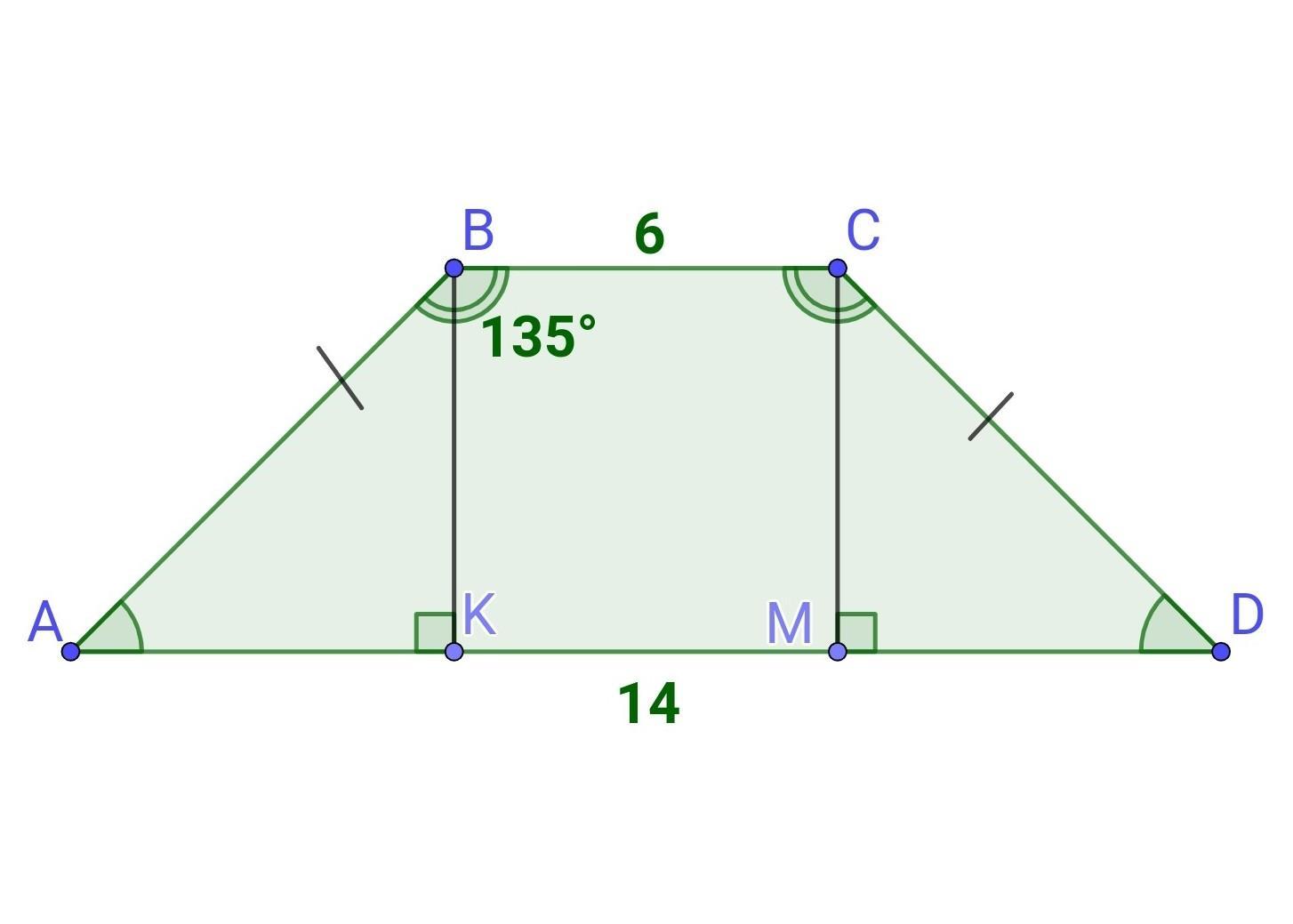
Основи рівнобічної трапеції дорівнюють 6 см і 14 см, а тупий кут-
135°. Знайди відстань між основами трапеції
У відповіді вкажи тільки число
Ответы
Ответ:
Відстань між основами трапеції дорівнює 4 см
Объяснение:
Основи рівнобічної трапеції дорівнюють 6 см і 14 см, а тупий кут - 135°. Знайди відстань між основами трапеції.
Відстанню між паралельними прямими називається довжина їхнього спільного перпендикуляра.
Розв'язання
1) Нехай ABCD - дана рівнобічна трапеція, BC||AD, AB=CD, BC=6см, AD=14см. ∠В=135°.
Так як BC||AD, то відстанью між цими прямими буде висота трапеції - довжина їхнього спільного перпендікуляра.
2) Проведемо висоти ВК і СМ. Отже, ∠AKB=∠CMD=90°.
Розглянемо △ABK і △DCM:
- АВ=CD - як бічні сторони рівнобічної трапеції
- ∠A=∠D - як кути при основі рівнобічної трапеції
Отже △ABK=△DCM за гіпотенузою і гострим кутом, а тому AK=DM.
3) Оскільки BKMC - прямокутник, то KM=BC=6(см).
Маємо:
(см)
4) Сума сусідніх кутів трапеції дорівнює 180°. Тому:
∠А=180°-∠В=180°-135°=45°.
5) В прямокутному трикутнику ABK за теоремою про суму гострих кутів прямокутного трикутника знайдемо кут АВК.
∠АВК=90°-∠А=90°-45°=45°, отже △ABK - рівнобедрений з основою АВ.
BK = AK = 4 (см) - як бічні сторони рівнобедреного трикутника.
#SPJ1