Предмет: Математика,
автор: mattilda493
доведіть тотожність 60б срочно
Приложения:
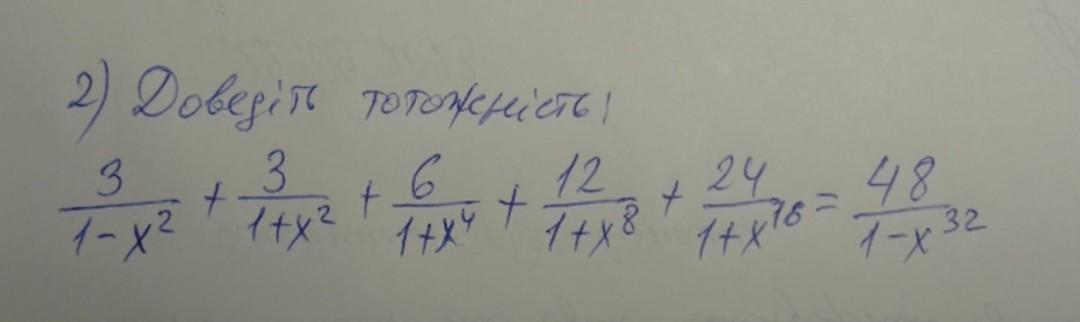
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
mattilda493:
спасибо большое
Похожие вопросы