Предмет: Геометрия,
автор: egortatarzin
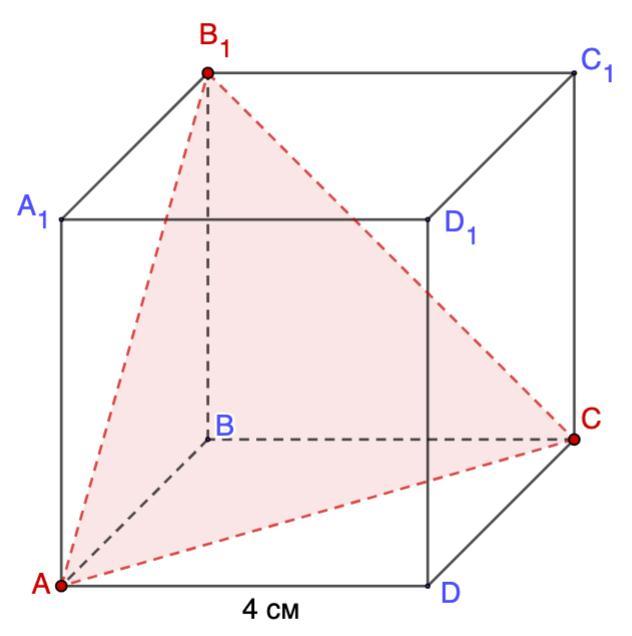
Изобразите сечение куба ABCDA,B,C,D, плоскостью, проходя- щей через вершины А, В и С. Найдите площадь полученного сечения, если ребро куба равно 4 см.
Приложения:

Ответы
Автор ответа:
4
Ответ:
Площадь сечения равна 8√3 см².
Объяснение:
Изобразите сечение куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через вершины А, В₁ и С. Найдите площадь полученного сечения, если ребро куба равно 4 см.
Построим сечение.
А ∈ (АА₁В₁); В₁ ∈ (АА₁В₁) ⇒ А и В₁ соединяем.
В₁ ∈ (ВВ₁С₁); С ∈ (ВВ₁С₁) ⇒ В₁ и С соединяем.
А ∈ (АВС); С ∈ (АВС) ⇒ А и С соединяем.
Получили сечение АВ₁С.
Дано: ABCDA₁B₁C₁D₁ - куб;
ΔАВ₁С - сечение;
АВ = 4 см.
Найти: S(АВ₁С)
Решение:
Грани куба - равные квадраты.
Стороны сечения - диагонали равных квадратов.
⇒ ΔАВ₁С - равносторонний.
Найдем длины сторон сечения.
- Диагональ квадрата найдем по формуле:
,
где а - сторона квадрата.
АС = 4 · √2 = 4√2 (см)
- Площадь равностороннего треугольника найдем по формуле:
Площадь сечения равна 8√3 см².
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: ulanka993
Предмет: Алгебра,
автор: artemsarukulov266
Предмет: Математика,
автор: kimanna3009
Предмет: Математика,
автор: bacmanliana
Предмет: Химия,
автор: hadaw10658
точки A и B1 лежат в одной плоскости
A и C лежат в одной плоскости
C и B1 лежат в одной плоскости,
то все эти точки соединяются отрезками
В сечении получается равносторонний треугольник так как его сторонами являются диагонали равных квадратов
Диагональ квадрата равняется 4√2 , площадь вычисляется по формуле а²√3/4
Имеем (16•2•√3)/4=8√3