Предмет: Математика,
автор: Rubakaplya
50 баллов Срочно. Помогите, пожалуйста, решить уравнение
Приложения:
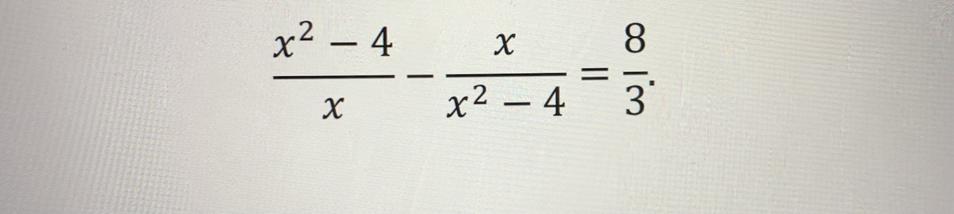
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
ОДЗ:
подставляем
Rubakaplya:
Спасибо большое
Похожие вопросы
Предмет: Литература,
автор: haliullinaskar37
Предмет: Литература,
автор: skyliees
Предмет: Математика,
автор: aisalkynaminamamatov
Предмет: ОБЖ,
автор: Аноним
Предмет: Алгебра,
автор: Overlord100lvl