Предмет: Геометрия,
автор: taniakupriy4
Площа поверхні октаедра, вершинами якої є точки перетину діагоналей граней куба, дорівнює 8Ѵ3 см². Знайдіть довжину ребра куба.
taniakupriy4:
tatyana_kupriy_
Ответы
Автор ответа:
4
Ответ:
Сторона куба равна 2√2 см.
Объяснение:
Площадь поверхности октаэдра, вершинами которой являются точки пересечения диагоналей граней куба, равна 8√3 см². Найдите длину ребра куба.
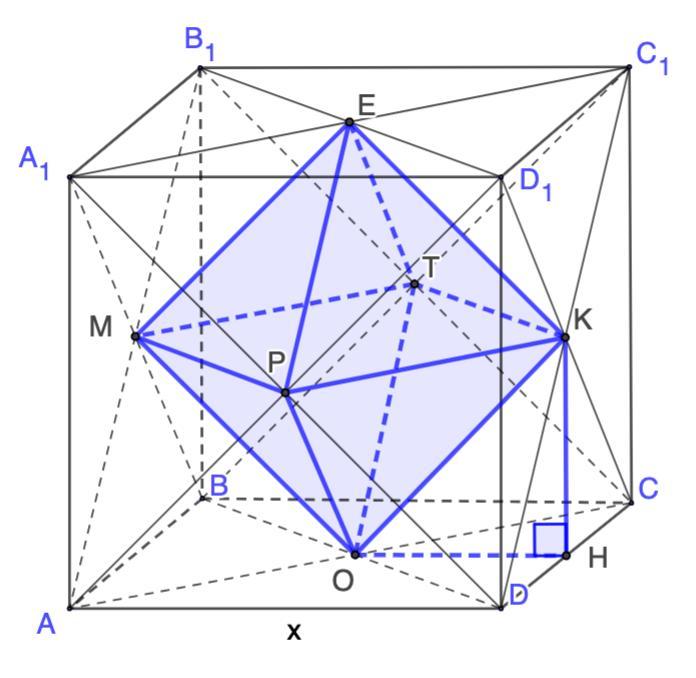
Дано: ABCDA₁B₁C₁D₁ - куб;
О, Е, Р, М, Т, К - точки пересечения диагоналей, вершины окиаэдра.
S окт = 8√3 см².
Найти: АВ
Решение:
- Формула поверхности октаэдра:
S пов. = 2a²√3,
где а - ребро октаэдра.
Подставим данные значения и найдем ребро октаэдра:
8√3 = 2а²√3 ⇒ а² = 4 ⇒ а = 2 см
Проведем КН⊥CD; соединим О и H.
Пусть сторона куба равна х см.
Рассмотрим ΔОКН - прямоугольный.
КН = ОН = х/2 (см)
По теореме Пифагора:
ОК² = КН² + ОН²
ОК = а = 2 см
Сторона куба равна 2√2 см.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: soyeonmylove4556
Предмет: Українська мова,
автор: talanovmaks2013
Предмет: Химия,
автор: polisukl335
Предмет: Алгебра,
автор: basok1978
Предмет: Математика,
автор: jerrymerry238