Предмет: Алгебра,
автор: kuksai934
Запишите выражение в виде степени с показателем степени 3(70 балов потому что час сижу не правильно получается
Приложения:

Alnadya:
в виде степени с показателем степени 3 ?
Ответы
Автор ответа:
1
Решение.
Применяем свойства степеней . Cмотри вложение .
Приложения:

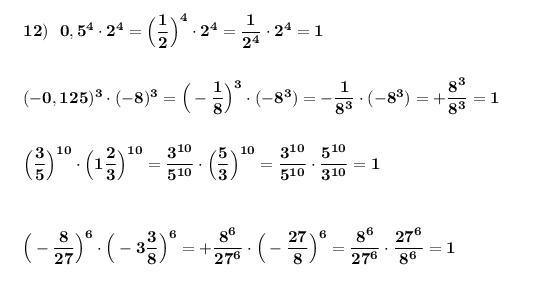

Похожие вопросы
Предмет: География,
автор: kiratsiopra
Предмет: Математика,
автор: alakosyk912
Предмет: Українська мова,
автор: cimbalm39
Предмет: Французский язык,
автор: shenwksh