ТЕРМІНОВО !
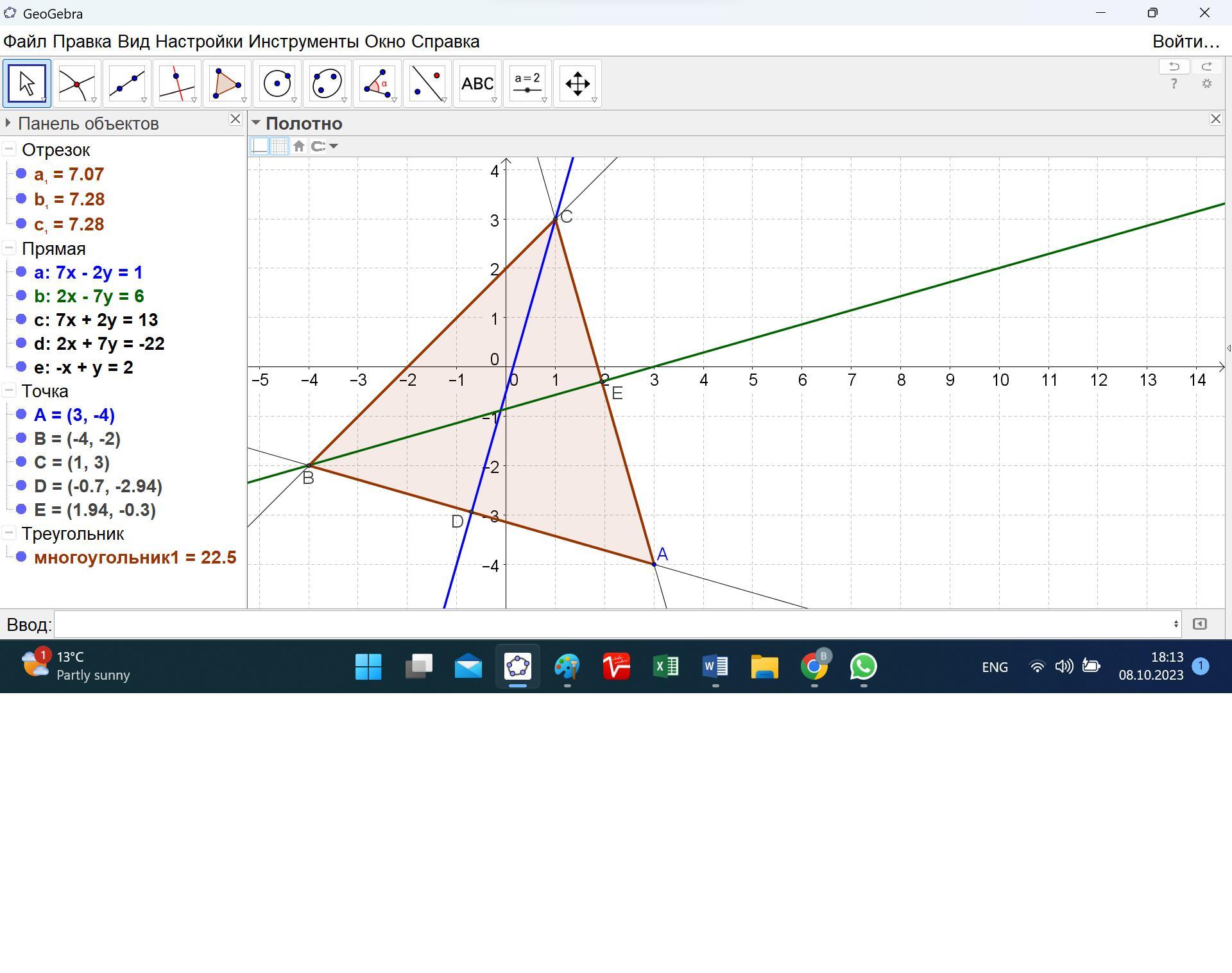
Скласти рівняння сторін трикутника ,знаючи вершину А(3;-4) та рівняння двох висот 7x-2y-1=0 i 2x-7y-6=0
Ответы
Скласти рівняння сторін трикутника ,знаючи вершину А(3;-4) та рівняння двох висот 7x-2y-1=0 (пусть это высота CD) i 2x-7y-6=0 (это высота BE).
Стороны треугольника – это перпендикуляры к заданным высотам.
К прямой с уравнением вида Ах + Ву + С = 0 в уравнении перпендикуляра коэффициенты А и В меняются на В и (-А) или (-В) и А.
К высоте 7x-2y-1=0 уравнение стороны будет 2х + 7у + С = 0.
Для определения параметра С надо подставить координаты точки А(3; -4).
2*3 + 7*(-4) + С = 0, отсюда С = 28 – 6 = 22.
Получаем уравнение стороны AB: 2х + 7у + 22 = 0.
Аналогично находим уравнение стороны AC.
К высоте 2x-7y-6=0 уравнение стороны будет 7х + 2у + С = 0.
Для определения параметра С надо подставить координаты точки А(3; -4).
7*3 + 2*(-4) + С = 0, отсюда С = 8 – 21 = -13.
Получаем уравнение стороны AB: 7х + 2у - 13 = 0.
Находим координаты точек В и С как точки пересечения заданных высот с найденными сторонами.
Точка В: 2x - 7y – 6 = 0 (1)
2х + 7у + 22 = 0 (2) (2) - (1)
14y + 28 = 0
y = -28/14 = -2.
x = (7y + 6)/2 = (7*(-2) + 6)/2 = (-14 + 6)/2 = -8/2 = -4.
Точка В(-4; -2).
Точка С: 7x - 2y – 1 = 0 (1)
7х + 2у - 13 = 0 (2) (2)- (1)
4y - 12 = 0
y = 12/4 = 3.
x = (2y + 1)/7 = (2*3 + 1)/7 = (6 + 1)/7 = 7/7 = 1.
Точка C(1; 3).
Теперь находим уравнение стороны ВС по координатам точек В(-4; -2) и C(1; 3).
(x + 4)/(1-(-4)) = (y + 2)/(3-(-2)),
(x + 4)/5 = (y + 2)/5 каноническое,
5х + 20 = 5у + 10
5х – 5у + 10 = 0
или х - у + 2 = 0 общее,
у = х + 2 с угловым коэффициентом.