Question

СРОЧНО!!!ДАМ 80 БАЛЛОВ!
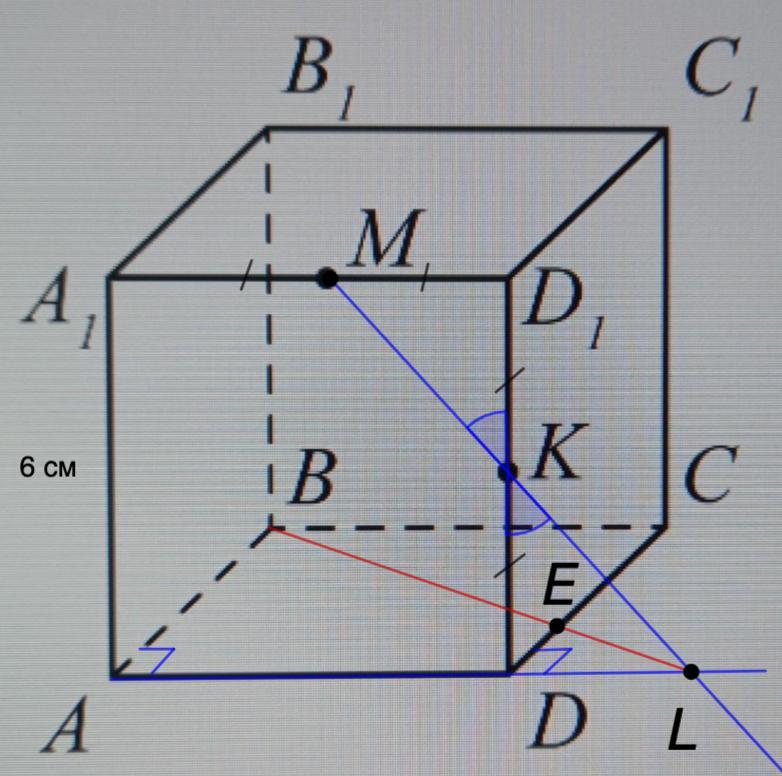
Точки М и К-середины ребер А1D1 и DD1 куба ABCDA1B1C1D1,ребро которого 6 см.Прямая МК пересекает плоскость АВС в точке L.Найдите длину отрезка LB.​

Answer 1

Ответ:

Длина отрезка  LB равна 3√13 см.

Объяснение:

Точки М и К - середины ребер А₁D₁ и DD₁ куба ABCDA₁B₁C₁D₁, ребро которого 6 см. Прямая МК пересекает плоскость АВС в точке L. Найдите длину отрезка LB.​

МК ∩ AD = L.

(AA₁D₁) ∩ (ABC) = AD   ⇒   AD ⊂ (ABC)

• Если прямая принадлежит плоскости, то все ее точки принадлежат этой плоскости.

⇒ МК ∩ (ABC) = L

Дано: ABCDA₁B₁C₁D₁ - куб;

A₁M = MD₁;   D₁K = KD;

AB = 6 см.

Найти: LB

Решение:

Рассмотрим ΔMD₁K и ΔLDK - прямоугольные.

D₁K = KD (условие)

∠МКD₁ = ∠LKD (вертикальные)

⇒ ΔMD₁K = ΔLDK (по катету и острому углу)

⇒ MD₁ = DL = 3 см

Рассмотрим ΔABL - прямоугольный.

АВ = 6 см;   AL = 6 + 3 = 9 (см)

• Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

⇒ LB² = AB² + AL² = 36 + 81 = 117

LB = √117 = 3√13 (см)

Длина отрезка  LB равна 3√13 см.

#SPJ1