Предмет: Математика,
автор: Nikita77713465
Ребят, решите пожалуйста. Даю 80 баллов.
Номера - 4.28, 2.29, 2.30
Приложения:
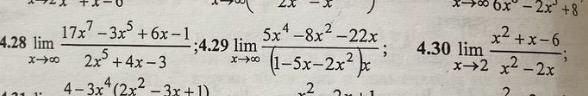
Nikita77713465:
4.28, 4.29, 4.30
Ответы
Автор ответа:
1
Ответ:
28. -3/2
29. -∞
30. 5/2
Пошаговое объяснение:
28
29
30
Похожие вопросы
Предмет: Математика,
автор: ditrixxlovehosinoai
Предмет: Қазақ тiлi,
автор: zanabergenkausar
Предмет: Українська література,
автор: lizasahraj63
Предмет: Литература,
автор: dollcandieq
Предмет: Математика,
автор: Аноним