Предмет: Математика,
автор: aagvrms
знайти фундаментальну систему розв'язків лінійної однорідної системи та записати її загальний розв'язок через цю фундаментальну систему
Приложения:
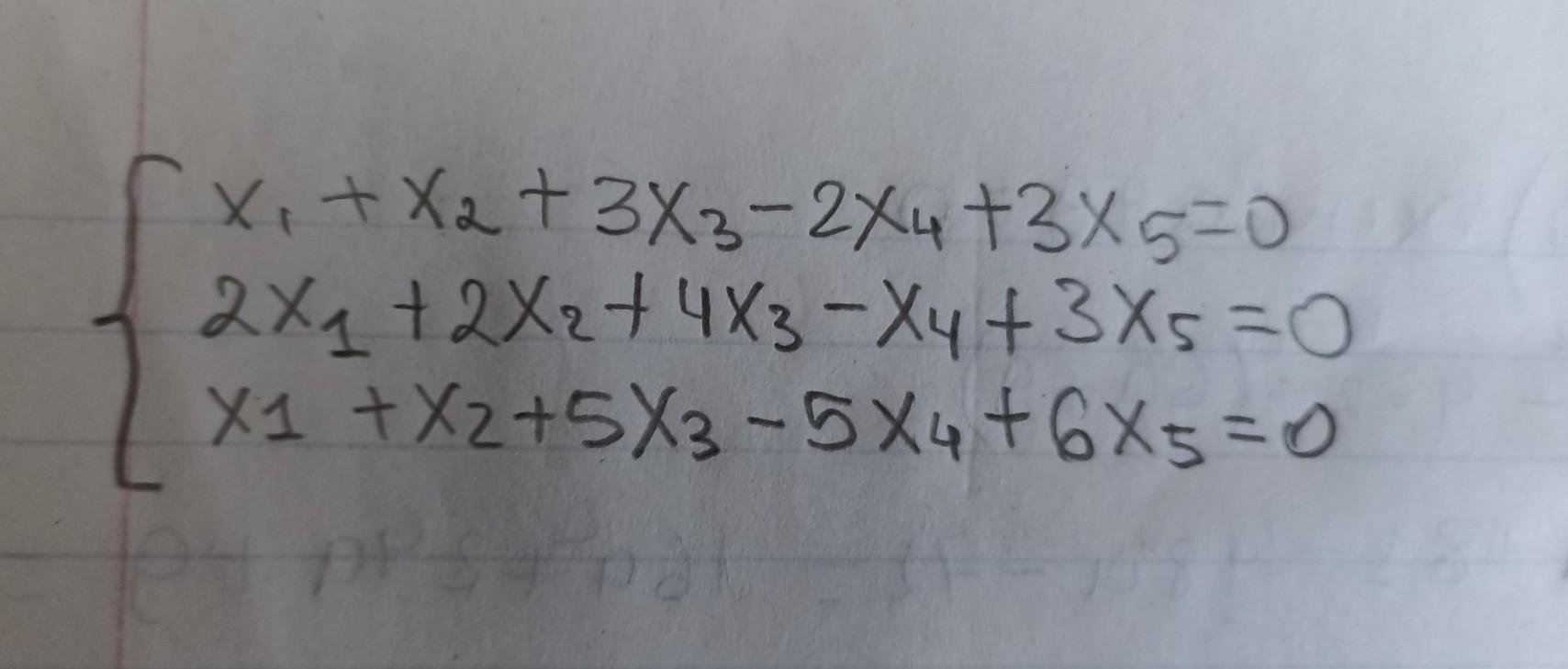
Ответы
Автор ответа:
2
Ответ:
Однородная система лин. уравнений .
Приведём матрицу системы к ступенчатому виду .
1) 1 стр. * (-2) + 2 стр . ; 3 стр. - 1 стр.
2) 2 стр. + 3 стр.
Базисные неизвестные : х₁ и х₃ , свободные неизвестные : х₂, х₄ , х₅
Свободные неизвестные обозначим х₂=2C₁ , х₄=2С₂ , х₅=2С₃ . Тогда решение запишем в виде
Фундаментальная система решений :
aagvrms:
дууууже дякую, якщо вам не важко, подивіться будь ласка і до інших завдань з матрицею в мене в запитаннях, буду дуже вдячна
Похожие вопросы