Предмет: Алгебра,
автор: diggercatch
Найти все целые решения неравенства (показательного)
Приложения:
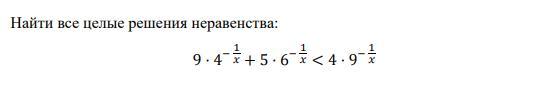
Ответы
Автор ответа:
0
Ответ:
неравенство не имеет целых решений
Объяснение:
Похожие вопросы
Предмет: Математика,
автор: tatianamandrykina073
Предмет: Українська мова,
автор: dasna17
Предмет: Английский язык,
автор: dianakosenko925
Предмет: История,
автор: vladakolt00
Предмет: Английский язык,
автор: anastasiazuravleva78