Предмет: Математика,
автор: shnoz0i0p0
Вычислите пожалуйста
Приложения:
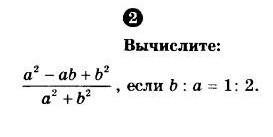
Ответы
Автор ответа:
1
Відповідь:Для выражения (а^2 - аb + b^2) / (a^2 + b^2), при условии b:a = 1:2, можно использовать подстановку. Пусть a = x, и тогда b = 2x (используя отношение b:a = 1:2). Теперь мы можем подставить это значение в выражение:
(а^2 - аb + b^2) / (a^2 + b^2) = (x^2 - x(2x) + (2x)^2) / (x^2 + (2x)^2)
Теперь упростим числитель и знаменатель:
Числитель: x^2 - 2x^2 + 4x^2 = 3x^2
Знаменатель: x^2 + 4x^2 = 5x^2
Теперь можем сократить общие множители:
(3x^2) / (5x^2) = 3/5
Таким образом, выражение (а^2 - аb + b^2) / (a^2 + b^2) при b:a = 1:2 равно 3/5.
Похожие вопросы
Предмет: Алгебра,
автор: krickijmikola81
Предмет: История,
автор: maksiprih
Предмет: Русский язык,
автор: omirxan000999111
Предмет: Математика,
автор: udarmodekhina
Предмет: Русский язык,
автор: zhandosmusenov2009