Question

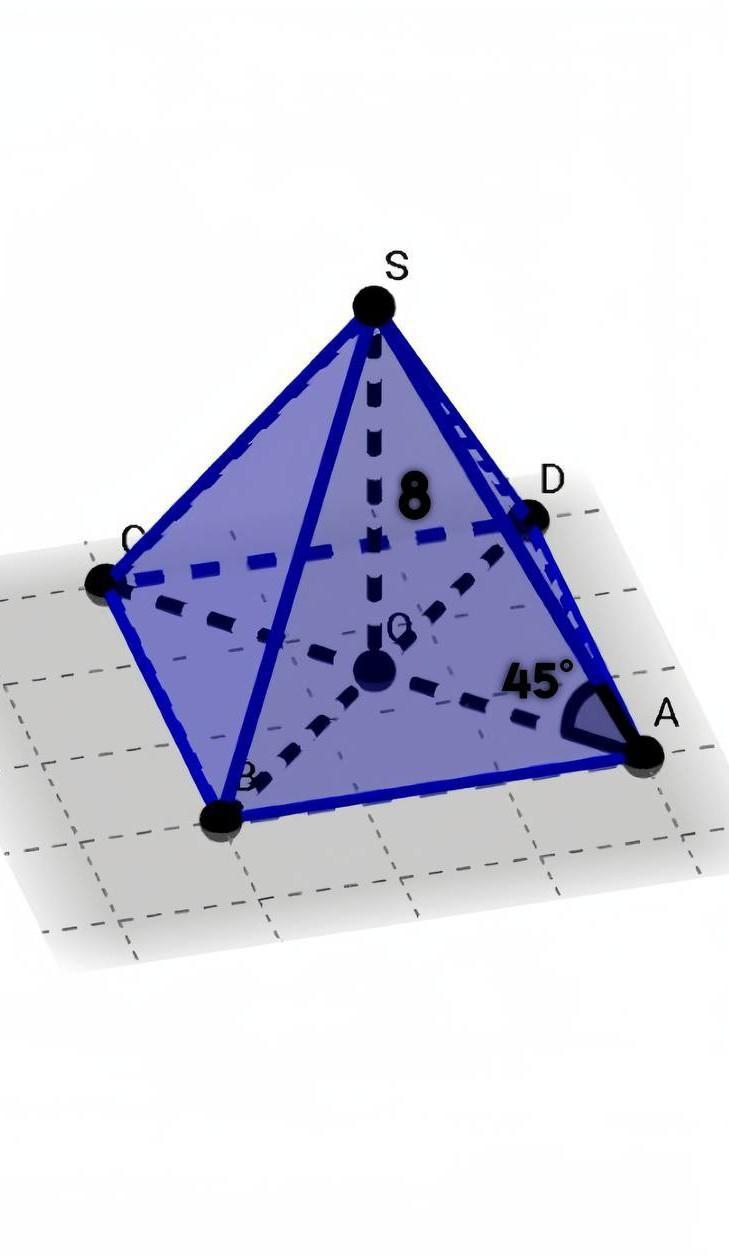
Висота правильної чотирикутної піраміди дорівнює 8 см, а бічне ребро нахилене до площини основи під кутом 45°. Знайдіть сторону основи піраміди.​

Answer 1

Ответ:

Сторона квадрата равна 8√2(см)

Объяснение:

Высота правильной четырехугольной пирамиды равна 8 см, а боковое ребро наклонено к плоскости основания под углом 45°. Найдите сторону основания пирамиды.

---------------------------------------------

Дано: SABCD – прав. четырех. пирамида, SO = 8(см), ∠SAO = 45°

Найти: АВ

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение

Т.к. пирамида правильная, то в основании лежит правильный многоугольник, в нашем случае квадрат. Проекция наклонной SA - OA, поэтому искомый угол ∠SAO. Найдем половину диагонали АО с помощью тангенса угла. Тангенс угла – это отношение противолежащего катета к прилежащему.

$\displaystyle \text{tg} \angle SAO = \frac{SO}{AO}$

$\displaystyle 1= \frac{8}{AO}$

$\displaystyle AO = 8(sm)$

АО = 8(см), тогда АС = 8 * 2 = 16(см)

Сторона квадрата в √2 раза меньше его диагонали:

$\displaystyle AB = \frac{16}{ \sqrt{2} } \:*\: \frac{ \sqrt{2} }{ \sqrt{2} }$

$\displaystyle AB = \frac{ \not16 \sqrt{2} }{ \not2 } = \boldsymbol{8 \sqrt{2}(sm)}$