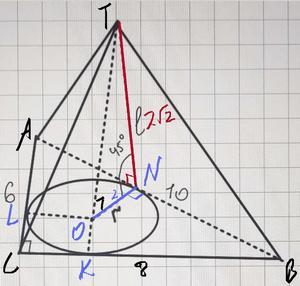
Допоможіть благаю!!! основою піраміди є прямокутний трикутник з катетами 6 см і гіпотинузою 10 см. Усі бічні грані піраміди утворюють з площиною основи кути по 45° . Знайдіть площу бічної поверхні піраміди
Ответы
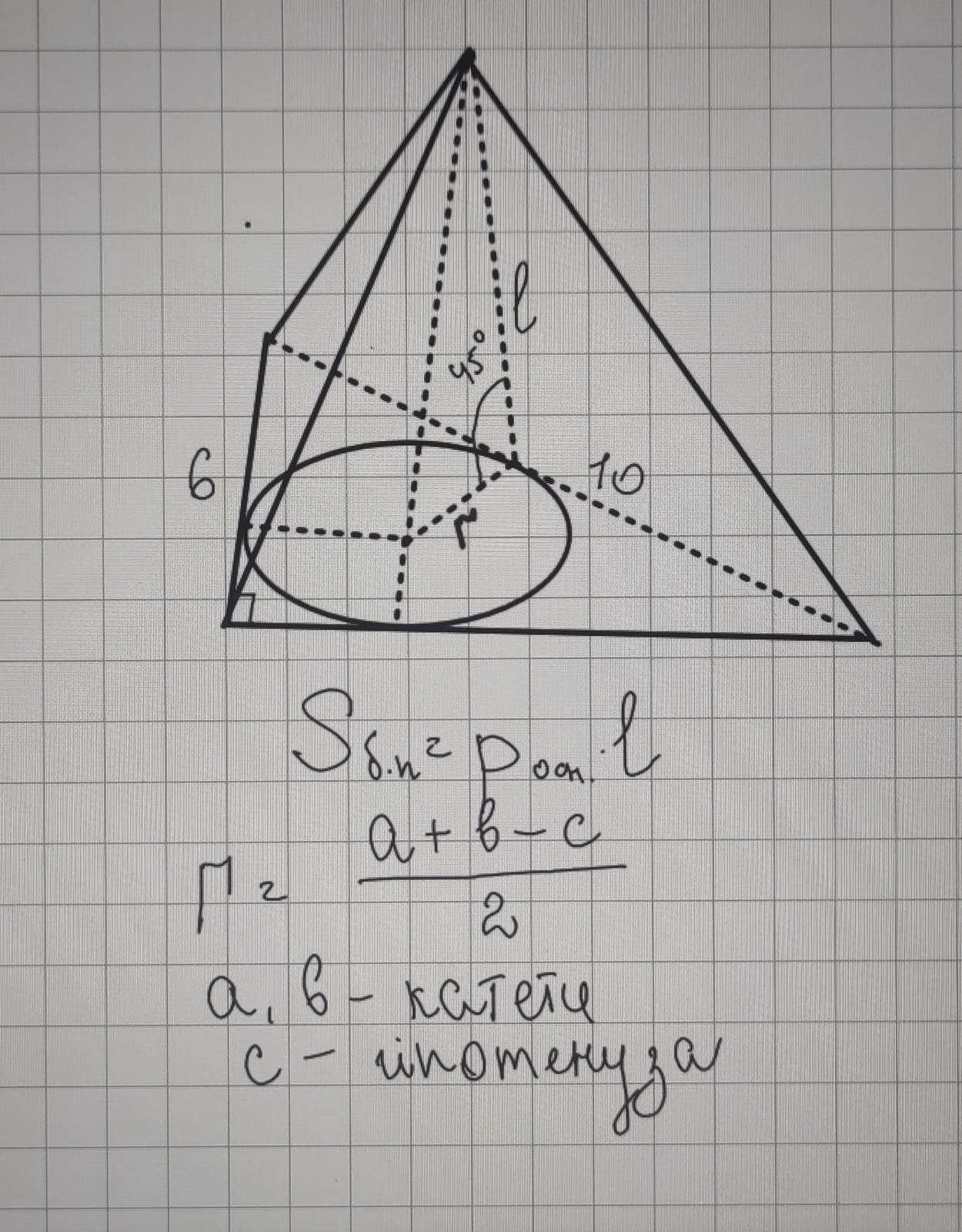
Обозначим пирамиду TABC
Опустим высоты боковых граней TK, TL, TN и высоту пирамиды TO.
По т о трех перпендикулярах OK, OL, ON - перпендикуляры к сторонам основания.
Угол между плоскостями - угол между перпендикулярами к общей прямой.
∠TKO, ∠TLO, ∠TNO - углы между боковыми гранями и основанием - по условию равны
=> △TKO=△TLO=△TNO (по катету и острому углу)
=> OK=OL=ON и TK=TL=TN
Доказали, что если боковые грани пирамиды наклонены к основанию под равными углами, то вершина падает в центр вписанной окружности основания и высоты боковых граней равны.
c=10, b=6
a=√(c^2-b^2) =8 (т Пифагора)
p=(a+b+c)/2 =12
r =(a+b-c)/2 =2
l =r/cos45 =2√2
Sбп =pl =24√2 (см^2)
Или рассмотрим основание как проекцию боковой поверхности.
S(ATB)=S(AOB)/cos45
S(ATC)=S(AOC)/cos45
S(BTC)=S(BOC)/cos45
Sбп =S(ABC)/cos45 =6*8/2 *√2 =24√2 (см^2)