Question

в треугольнике две стороны равны 5 см и 12 см,а синус угла между ними равен 2/5(дробью ). найдите площадь данного треугольника

Answer 1

пусть сторона в 12 см будет основанием (обозначим ее a).проекция второй стороны (обозначим ее b) на основание имеет длину 5 * 3/5 = 3 см.По теореме Пифагора высота треугольника h = sqrt(25-9) = 4 см.Площадь треугольника = S = ah/2 = 12*4/2 = 24 кв.см.Обозначим третью сторону c. Ее проекция на основание имеет длину = 12 - 3 = 9И по Пифагору ее длина = sqrt(16+81) = sqrt(97)Очевидно, что строна a=12 см самая большая в треугольнике, а значит максимальным будет угол ей противолежащий (т.е. угол между сторонами b и c)Площадь треугольника равен произведению длин сторон треугольника на половину синуса угла между ними, значит синус максимального угла равенsin A = S*2/(c*b) = 24*2/5/sqrt(97) = 9.6 / sqrt(97) Ответа) sqrt(97)б) 24в) 9.6 / sqrt(97)

Answer 2

Ответ:     12 см²

Объяснение:

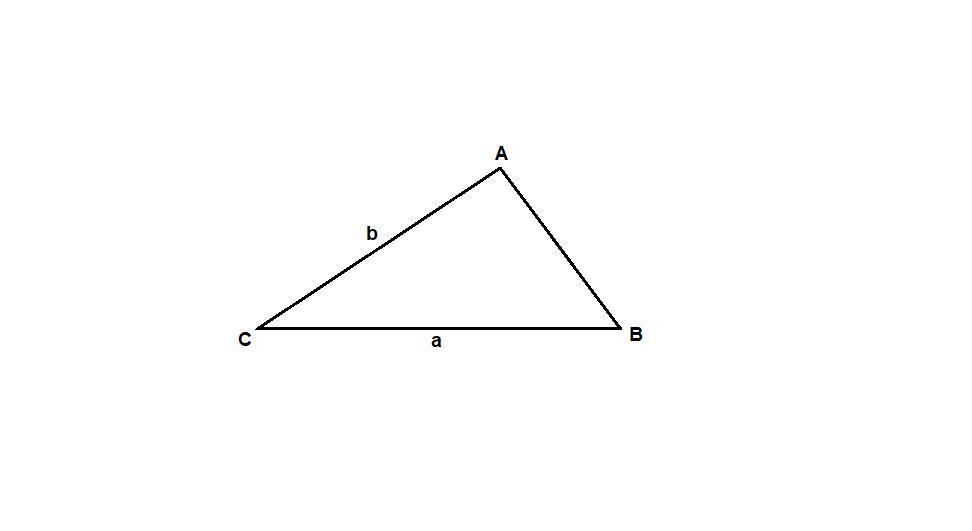
а = 5 см

b = 12 см

sin∠C = 2/5

Площадь треугольника можно найти как половину произведения двух сторон на синус угла между ними:

S = 1/2 ab·sin∠C

S = 1/2 · 5 · 12 · 2/5 = 12 см²