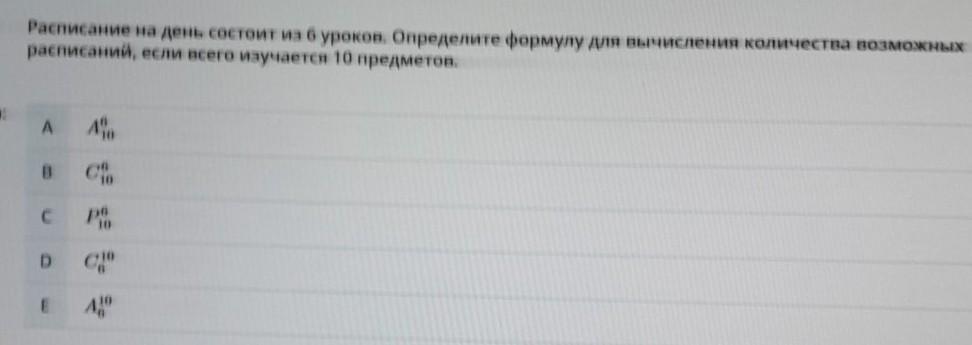
© 00:57:38 Расписание на день состоит из буроков. Определите формулу для вычисления количества всемохных расписаний, если всего изучается 10 предметов. 6 A A CO В C D E 10 10 10 АР
Ответы
Ответ:
Для вычисления количества возможных расписаний, если всего изучается 10 предметов, можно использовать формулу для сочетаний без повторений.
Формула для сочетаний без повторений:
C(n, k) = n! / (k!(n - k)!)
Где:
- n - общее количество элементов (10 предметов в данном случае).
- k - количество элементов, которые вы выбираете из общего количества (количество предметов в одном расписании в данном случае).
Если в одном расписании 6 предметов (бурок), то k = 6.
Теперь можем подставить значения в формулу:
C(10, 6) = 10! / (6!(10 - 6)!)
C(10, 6) = 10! / (6! * 4!)
C(10, 6) = (10 * 9 * 8 * 7 * 6!) / (6! * 4!)
Сокращаем 6!:
C(10, 6) = (10 * 9 * 8 * 7) / (4!)
Считаем факториал 4!:
C(10, 6) = (10 * 9 * 8 * 7) / (24)
C(10, 6) = 210
Итак, существует 210 различных расписаний, составленных из 10 предметов, где в каждом расписании 6 предметов.
Ответ:
Для вычисления количества возможных расписаний, где 10 предметов распределены на 6 уроков и порядок не имеет значения, используйте комбинации без повторений. Формула для этого выглядит так: C(n, r) = n! /(r!(n – r)!), где n – количество предметов (10), r – количество уроков (6), а C – комбинация без повторений. Подставим значение в формулу: C(10, 6) = 10! /(6!(10 - 6)!). Теперь вычислим значение: C(10, 6) = 10! /(6!*4!) = (10*9*8*7)/(4*3*2*1)=210. Итак, есть 210 возможных расписаний для 10 предметов на 6 уроков, где порядок не имеет значения.