Предмет: Алгебра,
автор: tddddrtdtddddd
3. Знайдіть невизначені інтеграли:
Приложения:
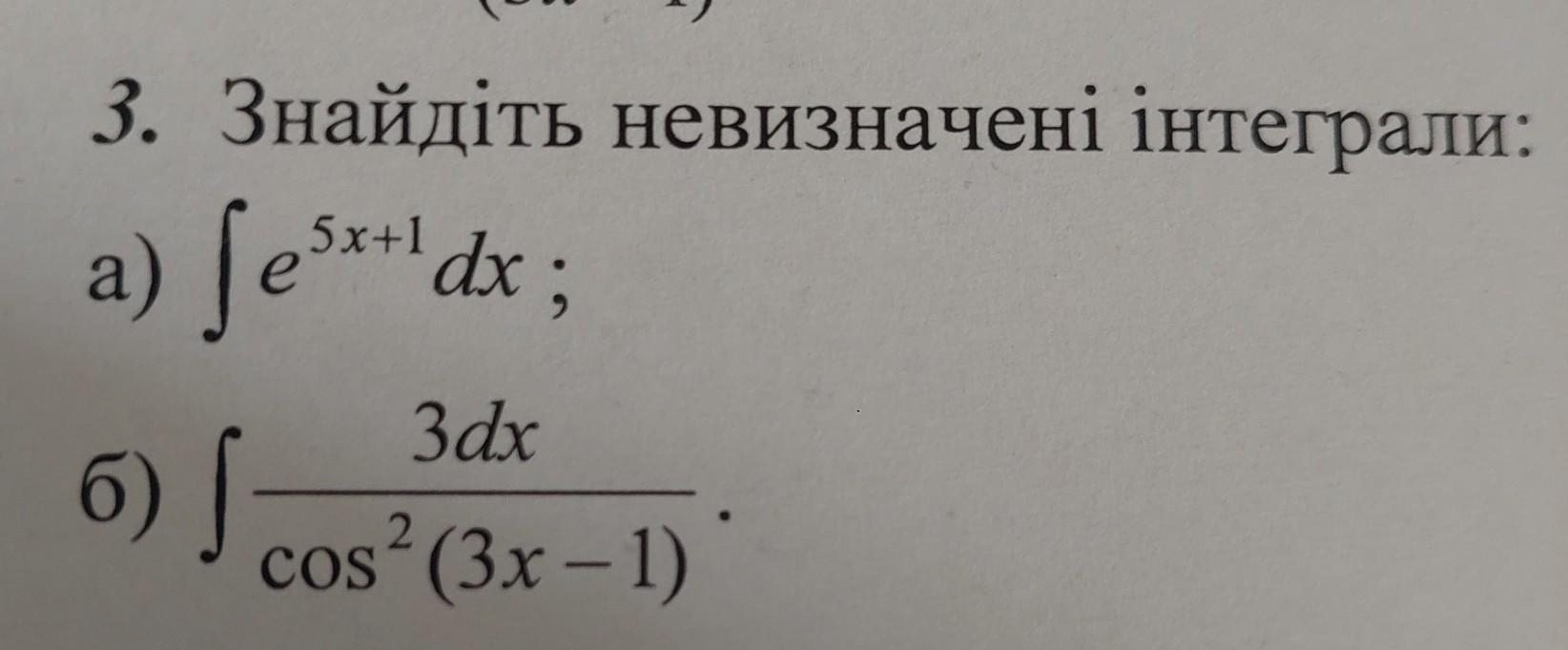
Ответы
Автор ответа:
1
Ответ:
a)1/5 e^(5x+1) + C
b)tg(3x-1) + C
Объяснение:
Т.к. степень экспоненты содержит сложную функцию, то неопределенный интеграл будет равен:
⠀⠀⠀⠀
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
⠀⠀⠀⠀⠀⠀
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
Вынесем константу:
Интеграл 1/cos²x = tgx + C, но у нас функция сложная, поэтому вместо "х" будет стоять весь аргумент косинуса.
Свойство:
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
Похожие вопросы
Предмет: История,
автор: alenaliashenko07
Предмет: История,
автор: zeinabiskan77
Предмет: Українська мова,
автор: taisiab173
Предмет: Информатика,
автор: 56ak
Предмет: Математика,
автор: turik0812