Question

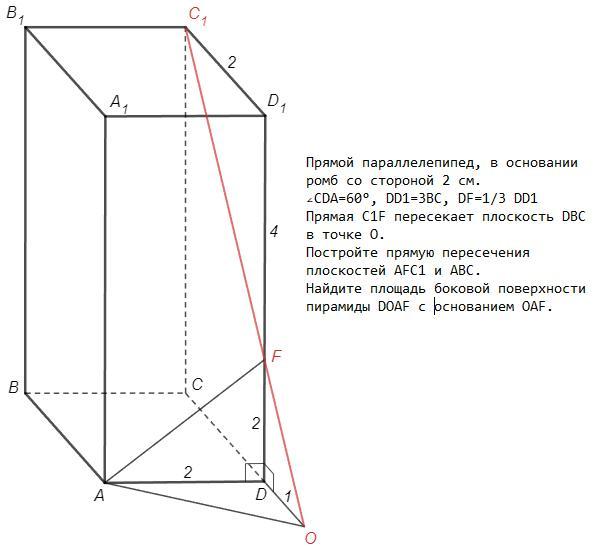
Основание прямого параллелепипеда ABCDA1BC1D1 - ромб, длина стороны которого равна 2 см. Точка F лежит на ребре DD1 так, что DF =1/3DD1 прямая C1F пересекает плоскость DBC в точке 0. Постройте прямую пересечения плоскостей AFC1, и АВС. Вычислите площадь боковой поверхности пирамиды DOAF с ocнованием 0AF, если уголCDA= 60°, DD1 = 3BC.

Answer 1

Плоскость AFC1 содержит прямую C1F. Прямая С1F пересекает плоскость ABCD в точке O. Таким образом плоскости AFC1 и ABC имеют общие точки A и O и общую прямую AO.

Прямая С1F лежит в плоскости СС1D1D, не совпадает с прямой C1D1, следовательно пересекает параллельную ей прямую CD. Прямая СD лежит в плоскости ABCD, С1F имеет с плоскостью ABCD только одну общую точку O, следовательно точка O лежит на прямой CD.

Все стороны ромба равны, основания призмы равны, BC=AD=C1D1=2

△С1FD1~△OFD (стороны параллельны)

DO/C1D1 =DF/D1F =1/2 => DO=1

Нашли точку O и прямую AO.

DF=DD1/3=3BC/3=BC =2

DD1⊥(ABC) (прямая призма) => DD1⊥AD, DD1⊥DO

S(ADF)=1/2 AD*DF =2

S(ODF)=1/2 DO*DF =1

∠ADO=180-∠CDA=120

S(ADO)=1/2 AD*DO sinADO =√3/2

Sбок =S(ADF)+S(ODF)+S(ADO) =3+√3/2