Question

Вычислить площадь треугольника, одна из вершин которого находится в полюсе, а две другие имеют полярные координаты А(4;π/4), В(1; 5π/18) в полярной системе координат. В ответ записать только числовое значение.

Answer 1

Ответ: 0,17453.

Объяснение:

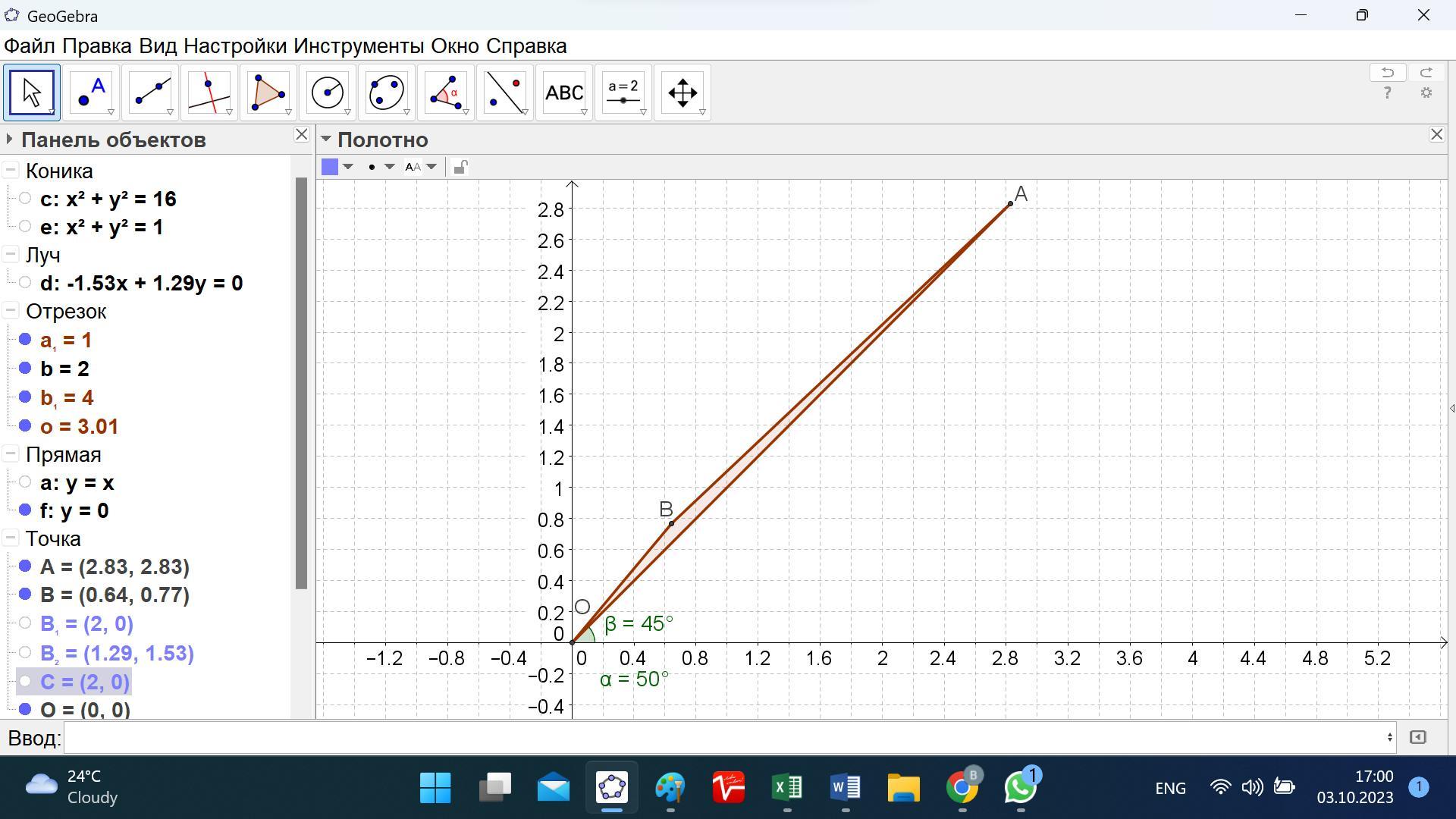
Площадь треугольника  находим как половину площади параллелограмма, построенного на радиус-векторах OA и ОВ.

По формулам находим прямоугольные координаты по известным полярным координатам.

x(A) =R*cos(fi) = 4*cos(pi/4) = 4*(√2/2) = 2√2.

y(A) =R*sin(fi) = 4*sin(pi/4) = 4*(√2/2) = 2√2.

x(B) =R*cos(fi) = 1*cos(5pi/18) = 1* 0.64278 = 0.64278.

y(B) =R*sin(fi) = 1*sin(5pi/18) = 1*  0.76604 =  0.76604.

Так как точка О имеет нулевые координаты, то координаты векторов ОА и ОВ численно совпадают с координатами точек А и В.

ОА = (2√2; 2√2), ОВ = (0.64278; 0.76604).

Площадь треугольника   по  радиус-векторам находим по формуле:

S(OAB) = (1/2)*r(A)*r(B)*sin(fi(B)-fi(A)) = (1/2)*4*1*sin((5pi/18)-(pi/4)) = 2*sin(pi/36) =  0,17453.