Предмет: Алгебра,
автор: karinkagolub8
Знайдіть площу криволінійної трапеції, зображеної на ри-
сунку
Приложения:
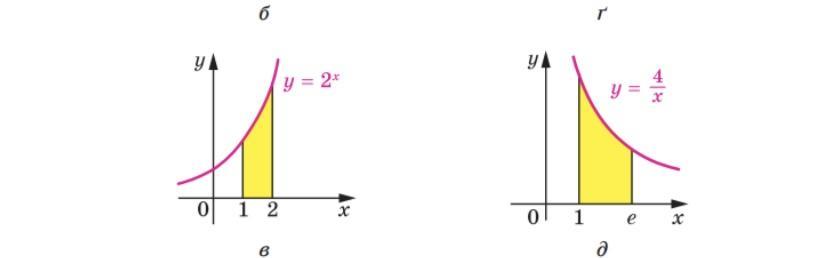
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Площадь криволинейной трапеции ищется с помощью определенного интеграла.
,
где у₀(х) - функция, график которой лежит "выше" на координатной плоскости; у₁(х) - функция, график которой лежит "ниже" на координатной плоскости.
Итак
Похожие вопросы
Предмет: Математика,
автор: prosyanoksofi
Предмет: Математика,
автор: karina04066813
Предмет: Алгебра,
автор: cacadacen
Предмет: Математика,
автор: artcrovvne
Предмет: Русский язык,
автор: ENotei