Предмет: Математика,
автор: bibos13
Решить 2 и 3 задание.
Буду очень благодарна .
Приложения:
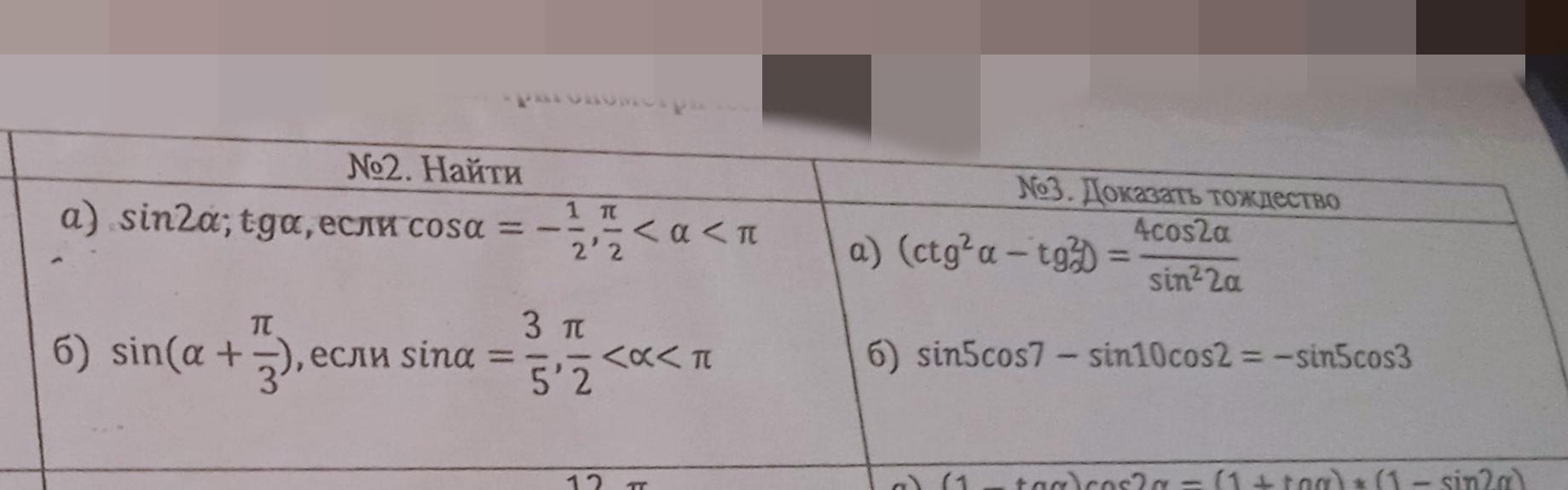
Ответы
Автор ответа:
1
Пошаговое объяснение:
Похожие вопросы
Предмет: Другие предметы,
автор: rozag8970
Предмет: История,
автор: cetttt65
Предмет: История,
автор: cwccvjz8mt
Предмет: Английский язык,
автор: diana734910
Предмет: Английский язык,
автор: yaroslavstebackov