Предмет: Алгебра,
автор: reccurent24
Відомо, що tgα=−5/12
і 3π/2<α<2π.
1) Якій чверті одиничного кола належить кут α?
2) Знайдіть значення cosα
3) Знайдіть значення sinα
Приложения:
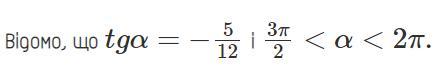
Ответы
Автор ответа:
8
1) α - угол четвёртой четверти , значит Cosα > 0 , Sinα < 0 .
Похожие вопросы
Предмет: Физика,
автор: mneda13
Предмет: Английский язык,
автор: citrus54citrus
Предмет: Английский язык,
автор: dotsenkos
Предмет: Физика,
автор: 1olyaka
Предмет: Литература,
автор: genius22136