Предмет: Алгебра,
автор: egor3665
20.4. Решите однородное тригонометрическое уравнение: 1) 4cos²x + sinxcosx + 3sin²x - 3 = 0; 2) cos²x - 3sinx cosx = -1; 3) 5sin’x – 3sinx cosx = 2cos²x; 4) 2sinx – 5sinx cosx = cos x – 2.
3 и 4 пожалуйста срочно умоляю срочно,даю 50 баллов!!!!
Приложения:
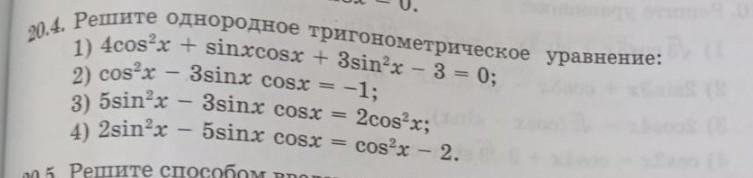
Ответы
Автор ответа:
5
Ответ:
если правильно то ставь лайк
Объяснение:
Воспользуемся основным тригонометрическим тождеством и преобразуем заданное уравнение, получим:
3 * sin² x - 3 * sin x * cos x - 4 * cos² x = -2,
3 * sin² x - 3 * sin x * cos x - 4 * cos² x = -2 * (sin² x + cos² x),
5 * tg² x - 3 * tg x - 2 = 0.
Получили квадратное относительно tg x уравнение, которое решается по элементарным формулам из курса алгебры (по формуле дискриминанта):
D = 9 + 40 = 49 = 7².
tg x = 1, откуда x = pi/4 + pi * k,
tg x = -2/5, откуда получим x = arctg (-2/5) + pi * k.
egor3665:
это какое?
3 или 4 ?
ты какое ваще решил? еклмн
Похожие вопросы
Предмет: Русский язык,
автор: nurgazymyngbay
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: vladislav9852
Предмет: Математика,
автор: rodhdhgd