Question

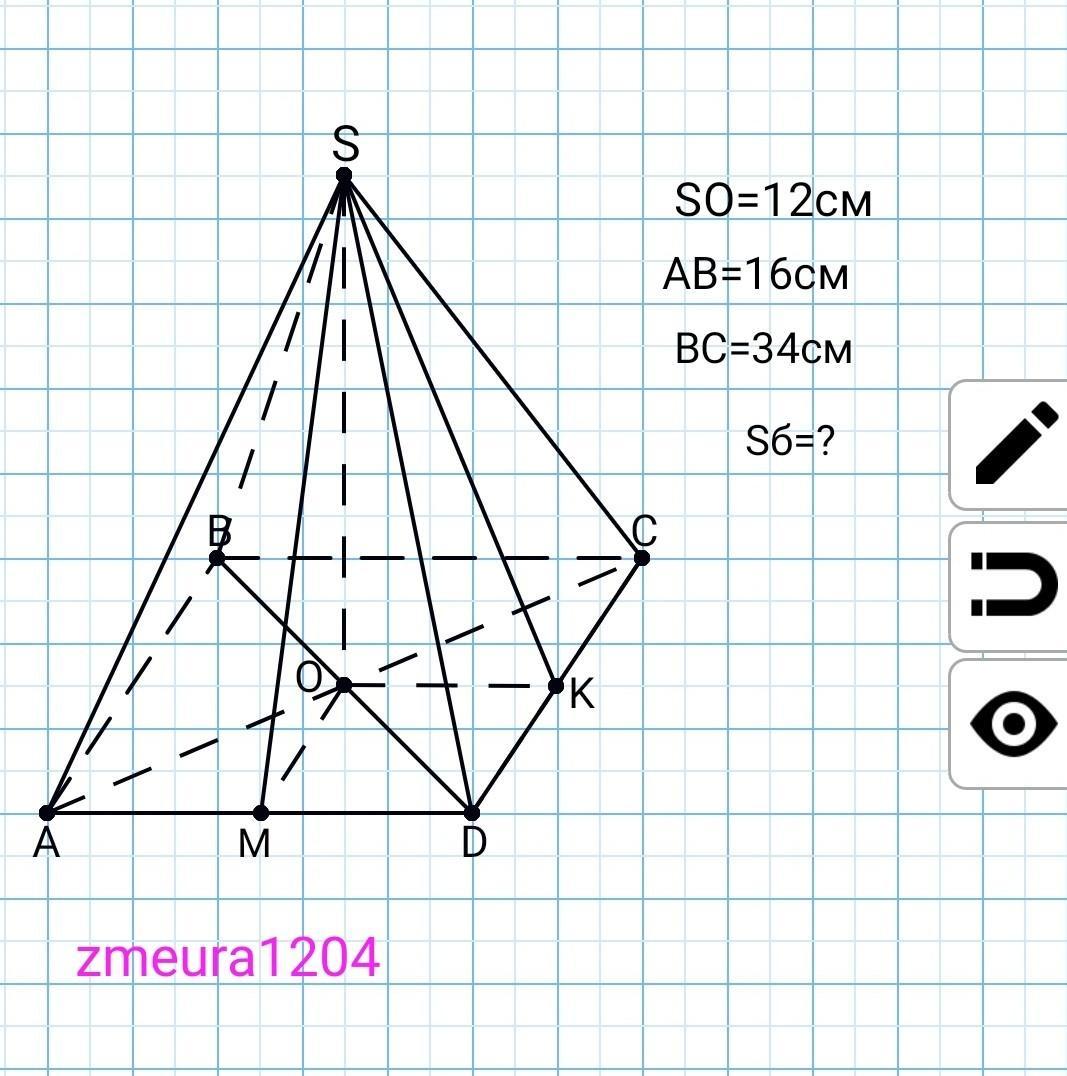
Основою чотирикутної піраміди є прямокутник зі сторонами 16 см і 34 см. Основою висоти піраміди є точка перетину Діагоналей прямокутника. Знайдіть площу бічної поверхні піраміди, якщо її висота дорівнює 12 см.

Answer 1

Ответ:

Площа бічної поверхні піраміди дорівнює 16√433+136√13см²

Объяснение:

ОК=ВС/2=34/2=17см.

∆SOK- прямокутний трикутник.

Теорема Піфагора:

SK=√(SO²+OK²)=√(12²+17²)=

=√(144+289)=√433см.

S(∆CSD)=½*CD*SK=½*16*√433=

=8√433 см²

ОМ=АВ/2=16/2=8см

∆SOM- прямокутний трикутник

За теоремою Піфагора:

SM=√(SO²+OM²)=√(12²+8²)=

=√(144+64)=√208=4√13см

S(∆SAD)=½*AD*SM=½*34*4√13=

=68√13см²

Sб=2*S(∆CSD)+2*S(∆SAD)=

=2*8√433+2*68√13=16√433+136√13см²