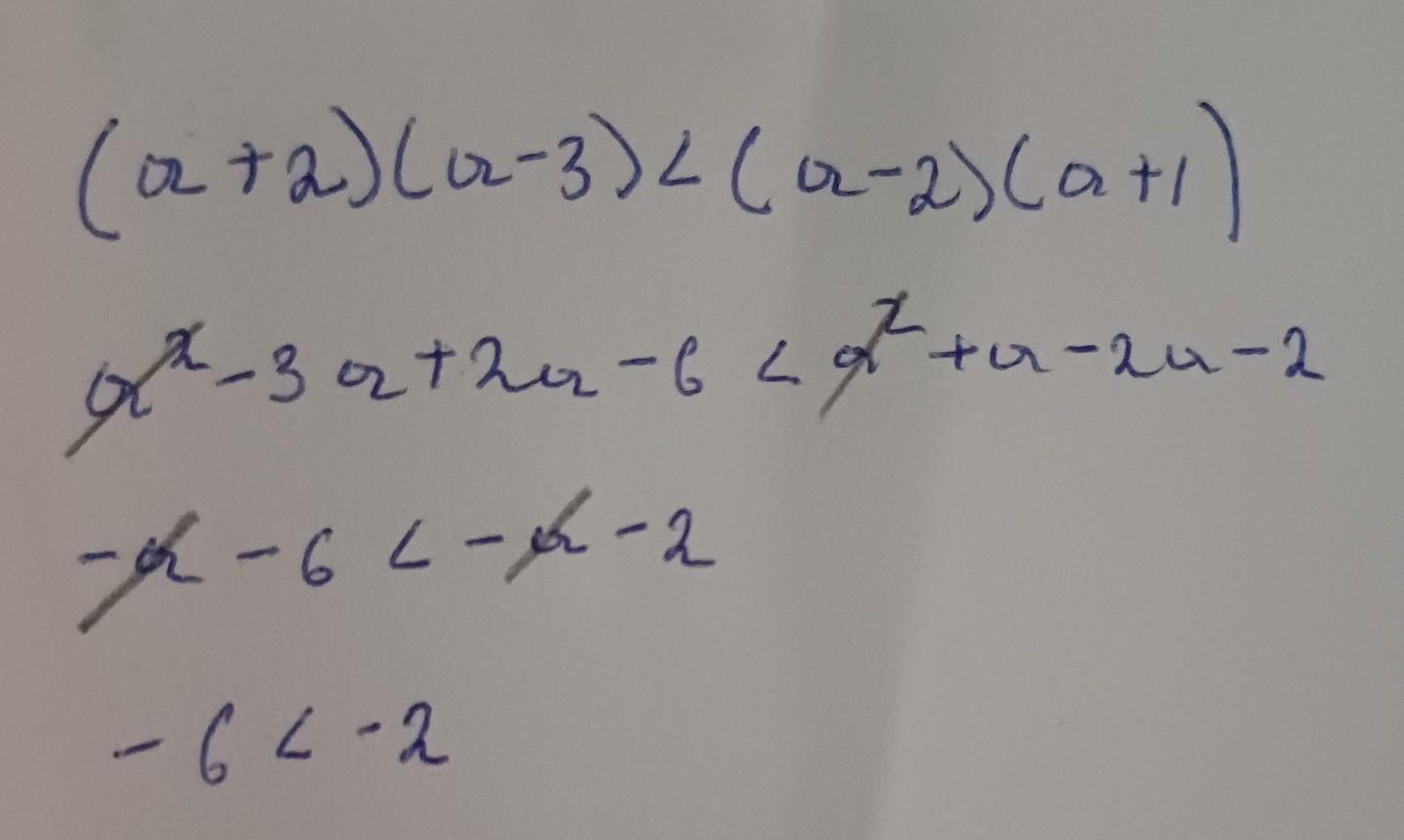Доведіть, що для всіх значень а виконується нерівність (a+2 (a-3) менше (a-2)(a+1)
Ответы
Ответ:
Щоб довести нерівність a + 2(a - 3) < (a - 2)(a + 1) для всіх значень a, спочатку розкриємо дужки та спростимо обидві частини нерівності:
a + 2(a - 3) < (a - 2)(a + 1)
a + 2a - 6 < a^2 - a - 2a - 2
3a - 6 < a^2 - 3a - 2
Тепер перенесемо всі члени на одну сторону нерівності, щоб отримати квадратичне нерівність:
a^2 - 6a - 3a + 2 - 6 < 0
a^2 - 9a - 4 < 0
Факторизуємо ліву частину:
(a - 4)(a + 1) < 0
Далі, скористаємося правилами знаків добутку:
1. a - 4 < 0 та a + 1 > 0
2. a - 4 > 0 та a + 1 < 0
Розв'язавши ці нерівності, отримуємо:
1. a < 4 та a > -1
2. a > 4 та a < -1
Оскільки в першому випадку a не може бути одночасно менше 4 і більше -1, а в другому випадку немає жодного значення a, що виконує обидві нерівності, то вихідна нерівність a + 2(a - 3) < (a - 2)(a + 1) справедлива для всіх значень a.
Ответ:
Утверждение справделиво для любого значения а