Предмет: Геометрия,
автор: spelll
Допоможіть благаю
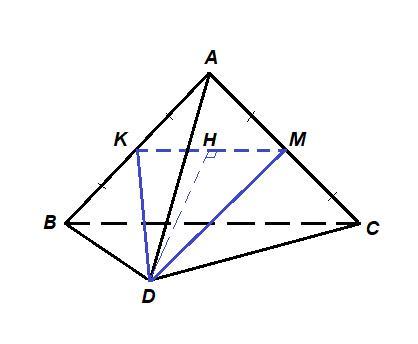
Побудуйте переріз правильного тетраедра ABCD площиною, яка проходить через вершину D і середини ребер AB та AC. Знайдіть периметр і площу перерізу, якщо AB = 3.
Ответы
Автор ответа:
1
Ответ:
Объяснение:
К - середина АВ, М - середина АС. Соединяем точки К, М и D.
KMD - искомое сечение.
а = АВ = 3.
КМ - средняя линия ΔАВС, равна половине ВС:
КМ = 0,5а = 1,5
DK и DM - медианы, а значит и высоты правильных треугольников ABD и ACD:
Периметр сечения:
ΔKMD равнобедренный, проведем к основанию КМ высоту DH. Она является так же медианой.
Из прямоугольного треугольника DKH по теореме Пифагора:
Площадь сечения:
Приложения:
Похожие вопросы
Предмет: Химия,
автор: apex4king777
Предмет: Українська мова,
автор: Аноним
Предмет: Қазақ тiлi,
автор: mevdokimova650
Предмет: Информатика,
автор: Аноним