Предмет: Физика,
автор: valeriachashina1010
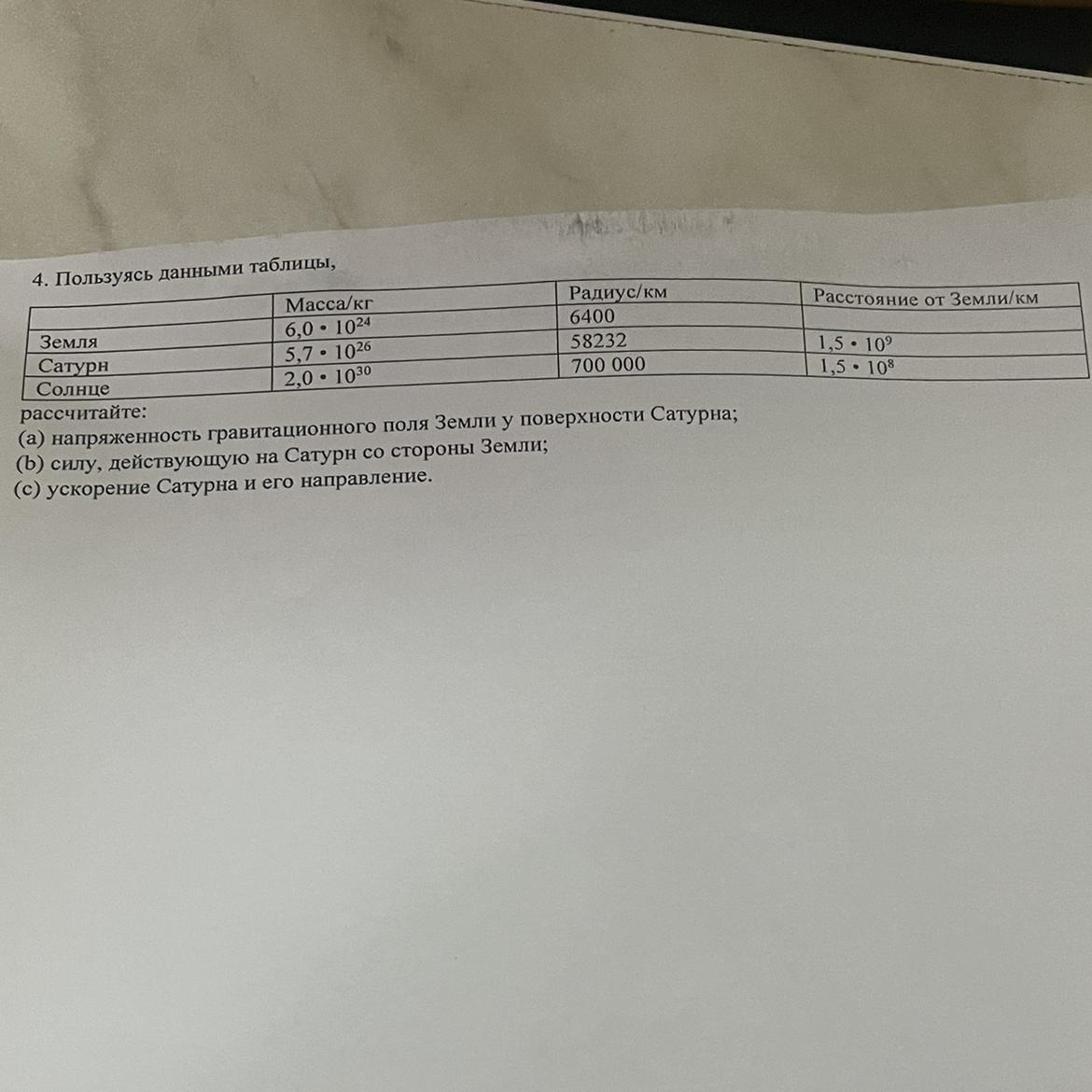
рассчитайте:
(а) напряженность гравитационного поля Земли у поверхности Сатурна;
(b) силу, действующую на Сатурн со стороны Земли; (с) ускорение Сатурна и его направление.
Приложения:
Ответы
Автор ответа:
2
Для расчетов используем закон всемирного тяготения Ньютона:
(a) Напряженность гравитационного поля (g) на поверхности Сатурна:
На Земле: g_земли ≈ 9.81 м/с²
Масса Сатурна (M_сатурна) ≈ 5.683 × 10^26 кг
Радиус Сатурна (R_сатурна) ≈ 58 232 км = 58 232 000 м
Используя формулу:
g_сатурна = G * M_сатурна / R_сатурна^2,
где G - гравитационная постоянная (приближенно 6.674 × 10^(-11) м³/(кг·с²)), можно рассчитать напряженность гравитационного поля на поверхности Сатурна:
g_сатурна ≈ 6.674 × 10^(-11) м³/(кг·с²) * 5.683 × 10^26 кг / (58 232 000 м)^2 ≈ 10.44 м/с².
(b) Сила, действующая на Сатурн со стороны Земли:
Формула для расчета силы F между двумя телами с массами M1 и M2 на расстоянии r друг от друга:
F = G * (M1 * M2) / r^2.
Масса Земли (M_земли) ≈ 5.972 × 10^24 кг
Расстояние между Землей и Сатурном (r) наиближшее ≈ 1 200 000 000 км = 1 200 000 000 000 м
Расчет силы:
F_земля-сатурн = 6.674 × 10^(-11) м³/(кг·с²) * (5.972 × 10^24 кг * 5.683 × 10^26 кг) / (1 200 000 000 000 м)^2 ≈ 3.7 × 10^18 Ньютонов.
(c) Ускорение Сатурна и его направление:
Ускорение Сатурна (a_сатурна) равно напряженности его гравитационного поля и будет направлено к центру планеты. Таким образом, ускорение Сатурна на его поверхности составляет приближенно 10.44 м/с² и направлено к центру Сатурна.
(a) Напряженность гравитационного поля (g) на поверхности Сатурна:
На Земле: g_земли ≈ 9.81 м/с²
Масса Сатурна (M_сатурна) ≈ 5.683 × 10^26 кг
Радиус Сатурна (R_сатурна) ≈ 58 232 км = 58 232 000 м
Используя формулу:
g_сатурна = G * M_сатурна / R_сатурна^2,
где G - гравитационная постоянная (приближенно 6.674 × 10^(-11) м³/(кг·с²)), можно рассчитать напряженность гравитационного поля на поверхности Сатурна:
g_сатурна ≈ 6.674 × 10^(-11) м³/(кг·с²) * 5.683 × 10^26 кг / (58 232 000 м)^2 ≈ 10.44 м/с².
(b) Сила, действующая на Сатурн со стороны Земли:
Формула для расчета силы F между двумя телами с массами M1 и M2 на расстоянии r друг от друга:
F = G * (M1 * M2) / r^2.
Масса Земли (M_земли) ≈ 5.972 × 10^24 кг
Расстояние между Землей и Сатурном (r) наиближшее ≈ 1 200 000 000 км = 1 200 000 000 000 м
Расчет силы:
F_земля-сатурн = 6.674 × 10^(-11) м³/(кг·с²) * (5.972 × 10^24 кг * 5.683 × 10^26 кг) / (1 200 000 000 000 м)^2 ≈ 3.7 × 10^18 Ньютонов.
(c) Ускорение Сатурна и его направление:
Ускорение Сатурна (a_сатурна) равно напряженности его гравитационного поля и будет направлено к центру планеты. Таким образом, ускорение Сатурна на его поверхности составляет приближенно 10.44 м/с² и направлено к центру Сатурна.
Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: Другие предметы,
автор: Limon2don
Предмет: Русский язык,
автор: matvejoseev86
Предмет: Математика,
автор: rasulmagametov4
Предмет: Физика,
автор: berezinskialeksandr