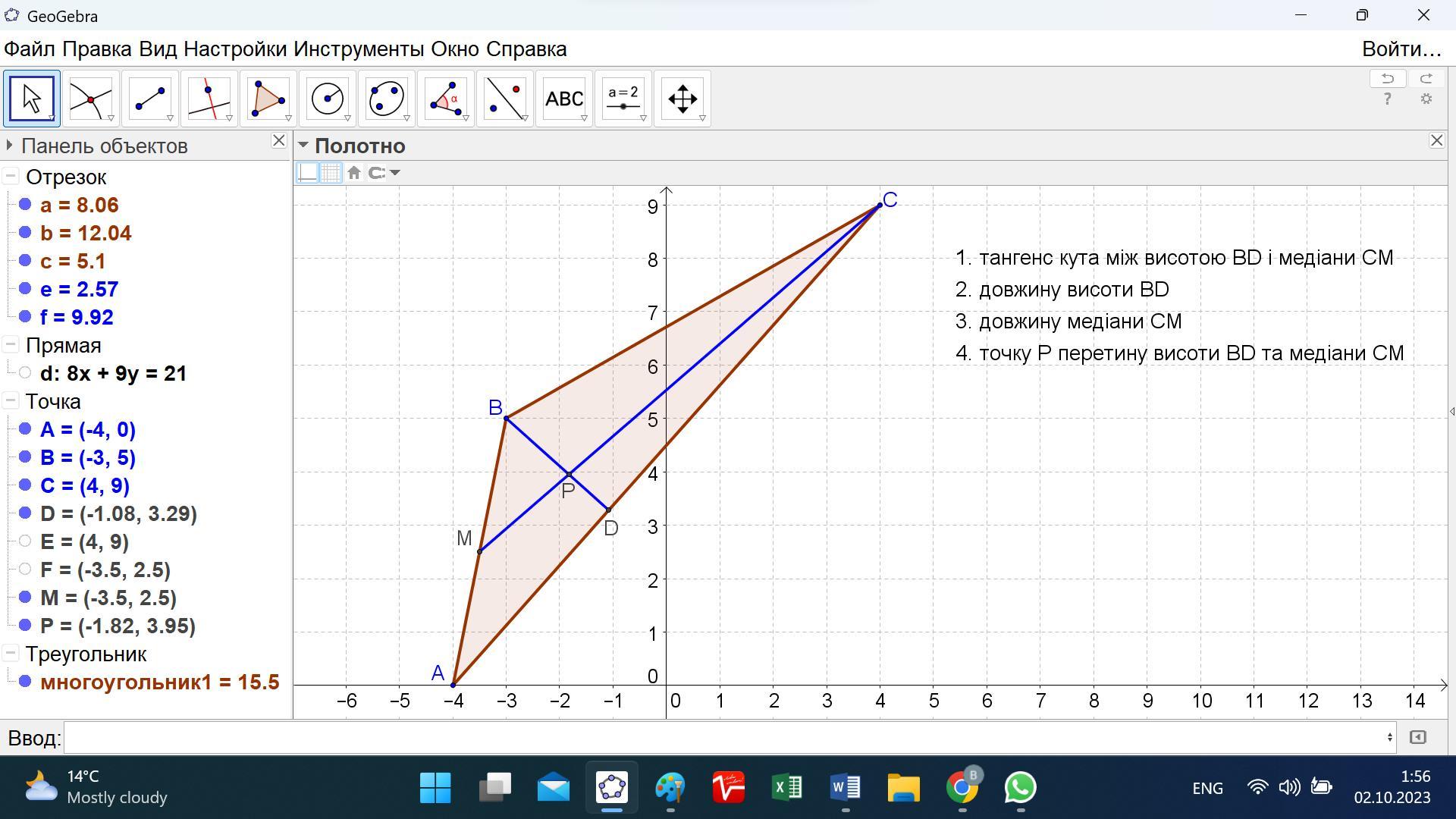
Дано трикутник ABC (Відомі координати вершин A B C D) A (-4 0) B (-3 5) C (4 9)
Знайти
1. тангенс кута між висотою BD і медіани CM
2. довжину висоти BD
3. довжину медіани СM
4. точку Р перетину висоти BD та медіани CM
(як я розумію точка D виходить з B, треба опустити)
Ответы
Полный ответ во вложении.
Пошаговое объяснение: большой объём информации и сложности с форматированием.
Даны точки A(-4; 0), B(-3; 5), C(4; 9).
1) Уравнение АС.
Вектор АС = (4-(-4); 9-0) = (8; 9).
Уравнение АС: (x +4)/8 = y/9,
9x + 36 = 8y,
9x – 8y + 36 = 0.
В уравнении перпендикуляра коэффициенты А и В меняются на (-В) и А.
8х + 9у + С = 0. Для определения С подставим координаты точки В(-3; 5).
8*(-3) + 9*5 + С = 0, отсюда С = 24 – 45 = -21.
Уравнение BD: 8x + 9y – 21 = 0.
Переходим к медиане СМ.
Координаты точки М как середины АВ:
М = ((-4-3)/2; (0+5)/2) = (-3,5; 2,5).
Вектор СМ = ((-3,5-4); (2,5-9) = (-7,5; -6,5).
Уравнение СМ: (х – 4)/(-7,5) = (у – 9)/(-6,5),
-6,5x + 26 = -7,5y + 67,5,
6,5x -7,5y + 41,5 = 0.
13x -15y + 83 = 0.
Угол φ между двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, вычисляется по формуле:
По формуле (дана во вложении) находим:
cos φ = 0.13
φ = arccos(0.13) = 82.550 градуса.
2) Находим координаты точки D как точку пересечения прямых ВD и АС.
BD: 8x + 9y – 21 = 0. х(8) = 64х + 72у – 168 = 0
АС: 9x – 8y + 36 = 0. Х(9) = 81х – 72у + 324 = 0.
145х + 156 = 0
х(D) = -156/145 ≈ -1,075862.
y(D) = (9х + 36)/8 = (9*(-156)/145) + 36)/8 = 3816/1160 = 477/145 ≈ 3,289655.
Находим длину высоты BD по координатам точек:
B(-3; 5), D((-156/145);(477/145)).
BD = √((-156/145)-(-3))² + ( (477/145)-5)²) = √(139345/21025) =
= 373,2894319/145 ≈ 2,57441.
Можно применить для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 формулу:
d = |A·Mx + B·My + C|/√(A² + B²)
Подставим в формулу данные:
d = |9·(-3) + (-8)·5 + 36|/√(9² + (-8)²)= |-27 - 40 + 36|/√(81 + 6) =
= 31/√145 = (31/145)·√145 ≈ 2,57441.
3) Координаты точки М найдены: М(-3,5; 2,5).
Находим длину медианы СМ по координатам точек:
C(4; 9) и М(-3,5; 2,5).
СМ = √((-3,5-4))² + (2,5-9)²) = √((-7,5))² + (-6,5)²) = √(56,25+42,25) =√98,5 ≈ 9,924717.
4) Находим координаты точки Р решением системы из уравнений прямых BD и CM.
BD: 8x + 9y – 21 = 0 x (15) = 120x + 135y – 315 = 0
СМ: 13x -15y + 83 = 0 x (9) = 117x – 135y + 747 = 0
237x - 0y + 432 = 0
x = -432/237 = -144/79 ≈ -1,822785.
y = (21 – 8x)/9 = (21 – 8*(-1,822785))/9 = 2811/711 = 937/237 ≈ 3,9535865.
Точка Р((-144/79);( 937/237)).