Предмет: Математика,
автор: nastqwep0
Виконайте дії будь ласка
Приложения:
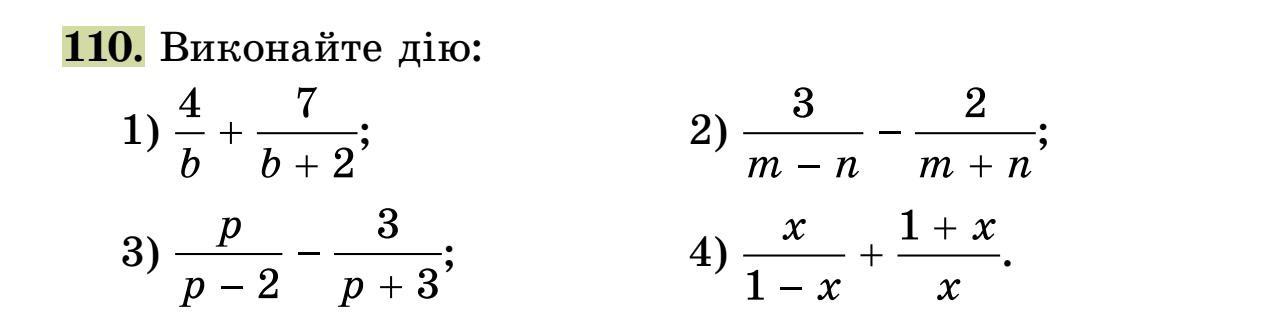
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: nothot144hz
Предмет: География,
автор: 10anastasiiaf
Предмет: Алгебра,
автор: ivanemelyanov2011
Предмет: Химия,
автор: karayevmustafa02
Предмет: Литература,
автор: Аноним