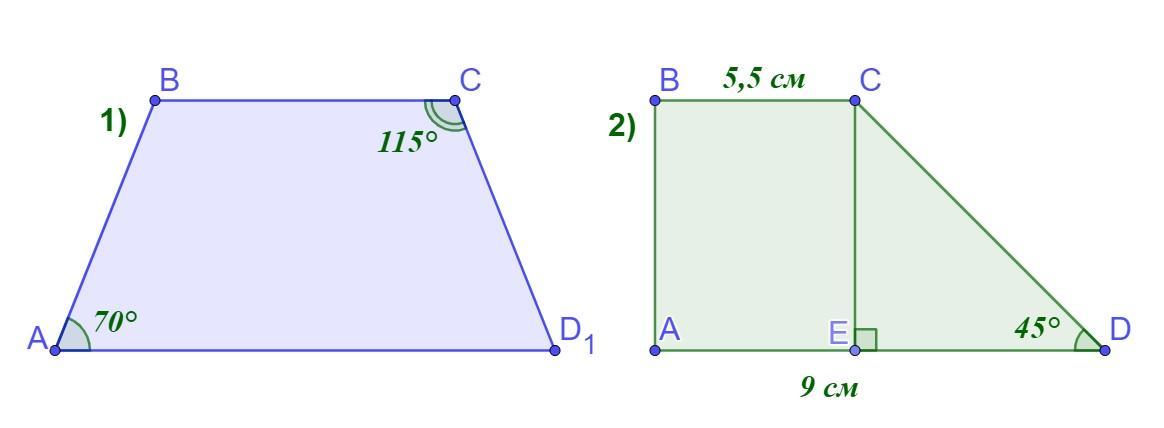
1) Два кути трапеції дорівнюють 115° і 70°. Знайди інші її кути.
2) Основи прямокутної трапеції дорівнюють 9 см і 5,5 см, а гострий кут 45°. Знайди довжину меншої бічної сторони. Распишите пожалуйста
Ответы
Ответ:
1) 110°, 65°
2) 3,5 см
Объяснение:
1) Два кути трапеції дорівнюють 115° і 70°. Знайди інші її кути.
2) Основи прямокутної трапеції дорівнюють 9 см і 5,5 см, а гострий кут 45°. Знайди довжину меншої бічної сторони.
1.
За властивістю трапеції, сума кутів, прилеглих до бічної сторони, дорівнює 180°. Так як сума заданих кутів ≠180°, то це протилежні кути трапеції ABCD.
Дано: ∠А = 70°, ∠С = 115°.
Знайти: ∠В, ∠D.
Розв'язання
1) ∠А + ∠В = 180° - як кути, прилеглі до бічної сторони трапеції, звідки
∠В = 180° - 70° = 110°
2) ∠С + ∠D = 180° - як кути, прилеглі до бічної сторони трапеції, звідки
∠D = 180° - 115° = 65°
Відповідь: 110°, 65°.
2.
Дано: ABCD -трапеція, AD||BC, AB⟂AD, AD = 9 см, ВС = 5,5 см, ∠D=45°.
Знайти: АВ
Розв'язання
1) Опустимо висоту CЕ на сторону AD, тобто СЕ⟂AD, (∠CED = 90°).
Так як ABCЕ - прямокутник, то АВ = СЕ, AE=BC=5,5(см) - як протилежні сторони прямокутника.
2) ED=AD-AE=9-5,5=3,5(см) - за аксиомою вимірювання відрізків.
3) Розглянемо ΔCED(∠E=90°).
∠ECD=90°-∠D=90°-45°=45° - за властивістю гострих кутів прямокутного трикутника.
∠ECD=∠D=45°, отже △CED - рівнобедрений з основою CD.
Тоді, CE = ED = 3,5 см - як бічні сторони рівнобедреного трикутника.
5) Отже, АВ = СЕ = 3,5 см.
Відповідь: 3,5 см
#SPJ1