Предмет: Алгебра,
автор: fi265is4i3
первообразная функции
подскажите пожалуйста как такое делать у меня не получилось...
Приложения:
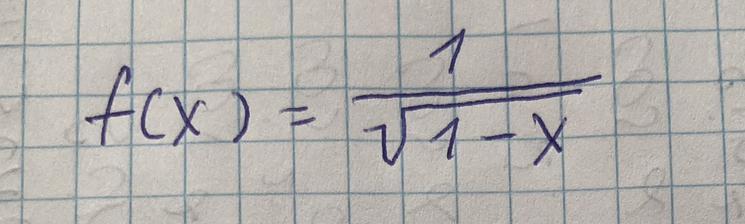
Ответы
Автор ответа:
1
Ответ:
Объяснение:
первообразная функция это антоним к вычислению производной (дифференцирование). Обычно такое проходит уже после производной, буду допускать что ты знаешь самую самую базу.
Открываешь таблицу интегралов и смотришь там формулы, на этом дело окончено. Тут точно также как в вычислений производной, только мы делаем обратное. Это как умножение и деление.
Учти что тут только верхушка айсберга, интегралы это очень обширная тема которую надо учить месяцами (а то и годами)
А что касается конкретно этого:
замена неудобных нам переменных: u = 1 - x, du = -dx
Выразить f(x) через u:
из той самой таблицы интегралов есть такая формула
работаем по ней
fi265is4i3:
спасибо за ваш ответ и время !
Похожие вопросы
Предмет: Математика,
автор: anastasiua1103
Предмет: Українська мова,
автор: slavacorbie2012
Предмет: География,
автор: holopikxxxkolin
Предмет: Английский язык,
автор: Laukersha22
Предмет: Математика,
автор: error65