Question

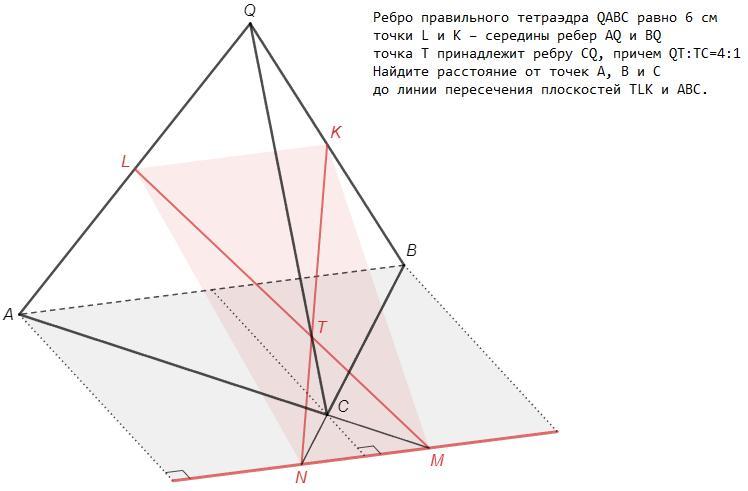
Ребро правильного тетраедра QABC дорівнює 6 см. Точки L і К - середини ребер АQ і BQ відповідно, точка Т належить ребру СQ, причому QT: TC = 4 : 1. Знайдіть відстань від точок А, В і С до лінії перетину площин TLK i ABC.

Answer 1

Пусть прямые LT и AC пересекаются в точке M

прямые KT и BC пересекаются в точке N.

M и N - общие точки плоскостей TLK и ABC, MN - общая прямая.

т Менелая

AL/LQ *QT/TC *CM/MA =1 => 1/1 *4/1 *CM/MA =1 => CM/MA=1/4

=> CM/AC =1/3

Аналогично CN/BC=1/3

△MCN~△ACB, k=1/3 (по двум пропорциональным сторонам и углу между ними)

MN||AB (накрест лежащие углы равны)

Расстояние от C до MN - высота △MCN

Расстояние от C до AB - высота △ACB

расстояния от A и B до MN - сумма высот △ACB и △MCN.

h(ACB) =AC sin60 =3√3

h(MCN) =h(ACB)/3 =√3

Ответ: (A;MN)=(B;MN)=4√3 (см) ; (C;MN)=√3 (см)