Предмет: Алгебра,
автор: kohsofi7
6.10 изобразите на координатной плоскости множество точек заданное системой неравенств :
Приложения:
Ответы
Автор ответа:
2
Ответ:
Объяснение:
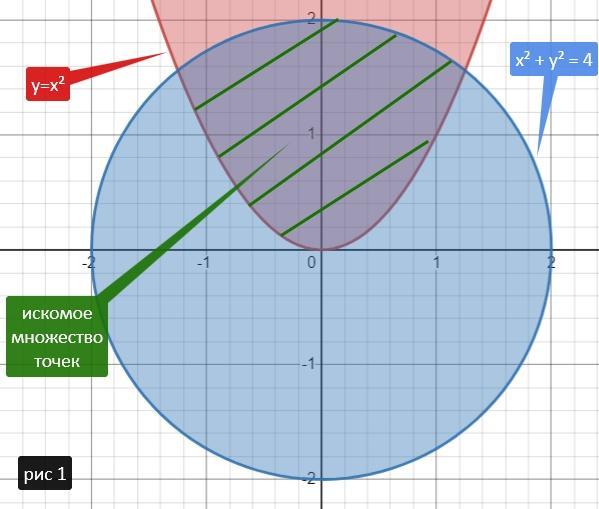
1)
y ≥ x² - это неравенство отображает все точки лежащие "внутри" параболы y=x²
x² + y² ≤ 4 - это неравенство отображает все точки, лежащие внутри круга с центром в (0; 0) радиусом 2
Рисуем эти области и пересечение этих областей даст нам искомое множество точек.
Сплошные линии показывают на то, что границы фигур входят в множество точек.
Рисунок 1
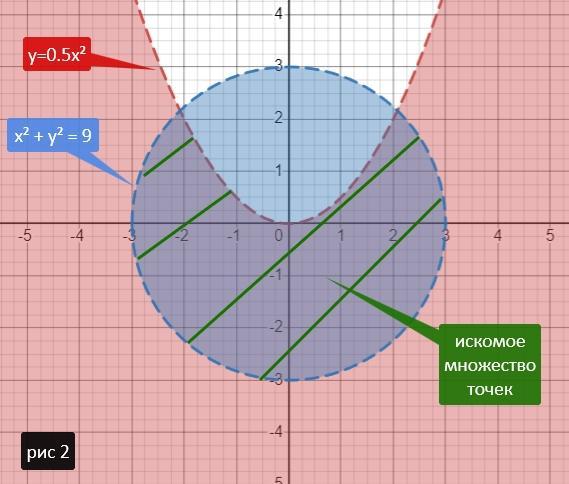
2)
y < 0.5 x² - это неравенство отображает все точки лежащие "bpdyt" параболы y=0.5x²
x² + y² < 9 - это неравенство отображает все точки, лежащие внутри круга с центром в (0; 0) радиусом 3
Рисуем эти области и пересечение этих областей даст нам искомое множество точек.
Пунктирные линии показывают на то, что границы фигур не входят в множество точек.
Рисунок 2
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: barnilycufer
Предмет: Биология,
автор: antonlobanov0710
Предмет: Математика,
автор: lera91460
Предмет: Қазақ тiлi,
автор: nastya666sukrusheva
Предмет: Геометрия,
автор: amina0720