Предмет: Математика,
автор: anonimus218
Найдите все а при каждом из которых система уравнений имеет единственное решение
Приложения:
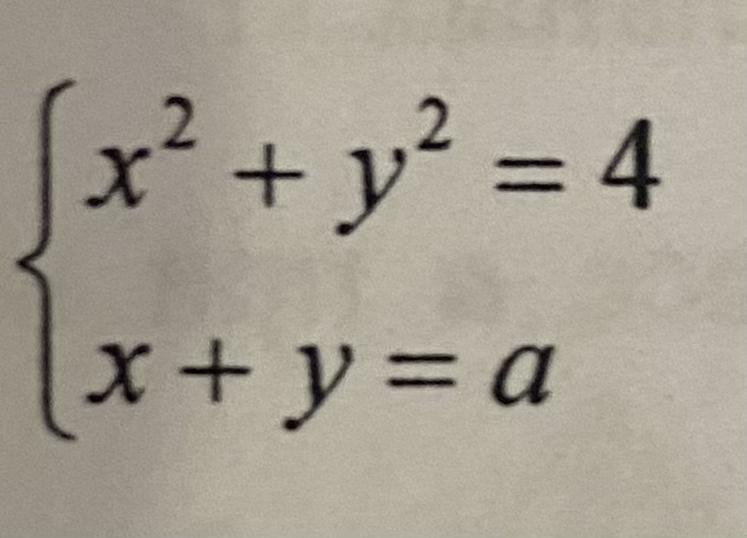
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Cистема имеет единственное решение, когда дискриминант равен нулю.
Похожие вопросы
Предмет: Английский язык,
автор: nnniiiixxskwq
Предмет: Математика,
автор: daniamereke4
Предмет: Русский язык,
автор: elina241604
Предмет: Биология,
автор: bosoevakatya
Предмет: Физика,
автор: 2006veronika2006