Предмет: Алгебра,
автор: Liza1864
Знайдіть найбільше ціле число, яке задовольняє нерівність
Приложения:
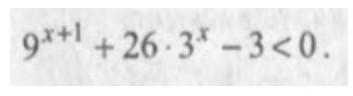
Ответы
Автор ответа:
1
Решение .
Найти наибольшее целое число, которое удовлетворяет неравенству :
Замена: , тогда
Неравенство перепишем в виде :
Переходим к старой переменной , делаем обратную замену .
Ответ: наибольшее целое решение неравенства - это х = -1 .
Приложения:

Похожие вопросы
Предмет: Українська мова,
автор: glovamaksim
Предмет: Физика,
автор: skibcikvalentin21
Предмет: Математика,
автор: adilcaybasarskiy
Предмет: Алгебра,
автор: alhamzat14
Предмет: Русский язык,
автор: ivangoshkovich2007