В прямоугольной трапеции меньшее основание равно 6, а меньшая боковая сторона 2квадратных корня из 3. Найти площадь трапеции, если один из её углов равен 120 градусов
Ответы
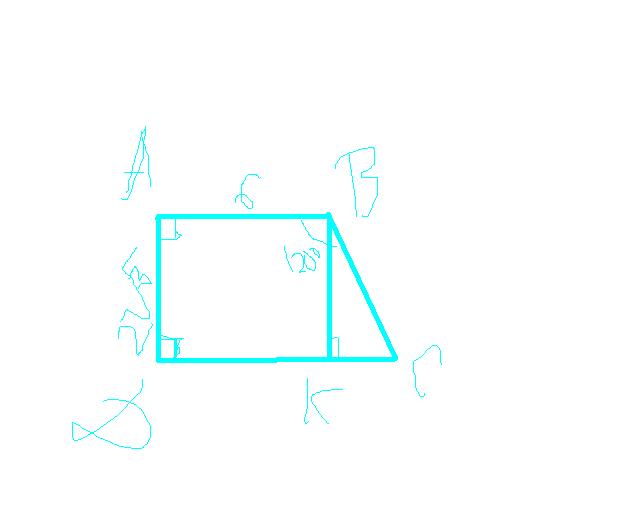
Трапеция АВСD, углы А и В равны по 90, угол С=120. Провести высоту СN из точьки С и она равна корень квадратный из з-х.После того как провели высоту получается квадрат и прямоугольный треугольник CND B=90,C=30, D=60 По синусу находим гепотену, она равна отношению противолежащего катета, в нашем слусае CN к гипотенузе CD. Выражаем гипотенузу. И она равна 2. Отрезок CN=1, из-за угла в зо градусов. Находим площадь ((6+7)/2)*двадратный корень из 3-х. Равно 6,5корень из 3-х.
Пусть АВСD - данная трапеция, AB=6, AD=2*корень(3), угол АВС=120 градусов,
проведем высоту ВК
тогда угол KBC=120-90=30 градусов
угол С=90-30=60 градусов
BK=AD=2*корень(3)
DK=AB=6
по соотношениям в прямоугольном треугольнике
BK/CK=tg C
СК=BK/ tg C
CK=2*корень(3)/tg 60=2*корень(3)/корень(3)=2
CD=CK+DK=6+2=8
Площадь трапеции равна произведению ее высоту на полусумму ее оснований
S=(AB+CD)/2 *AD
S=(6+8)/2*2*корень(3)=14*корень(3)