Помогите пожалуйста дж
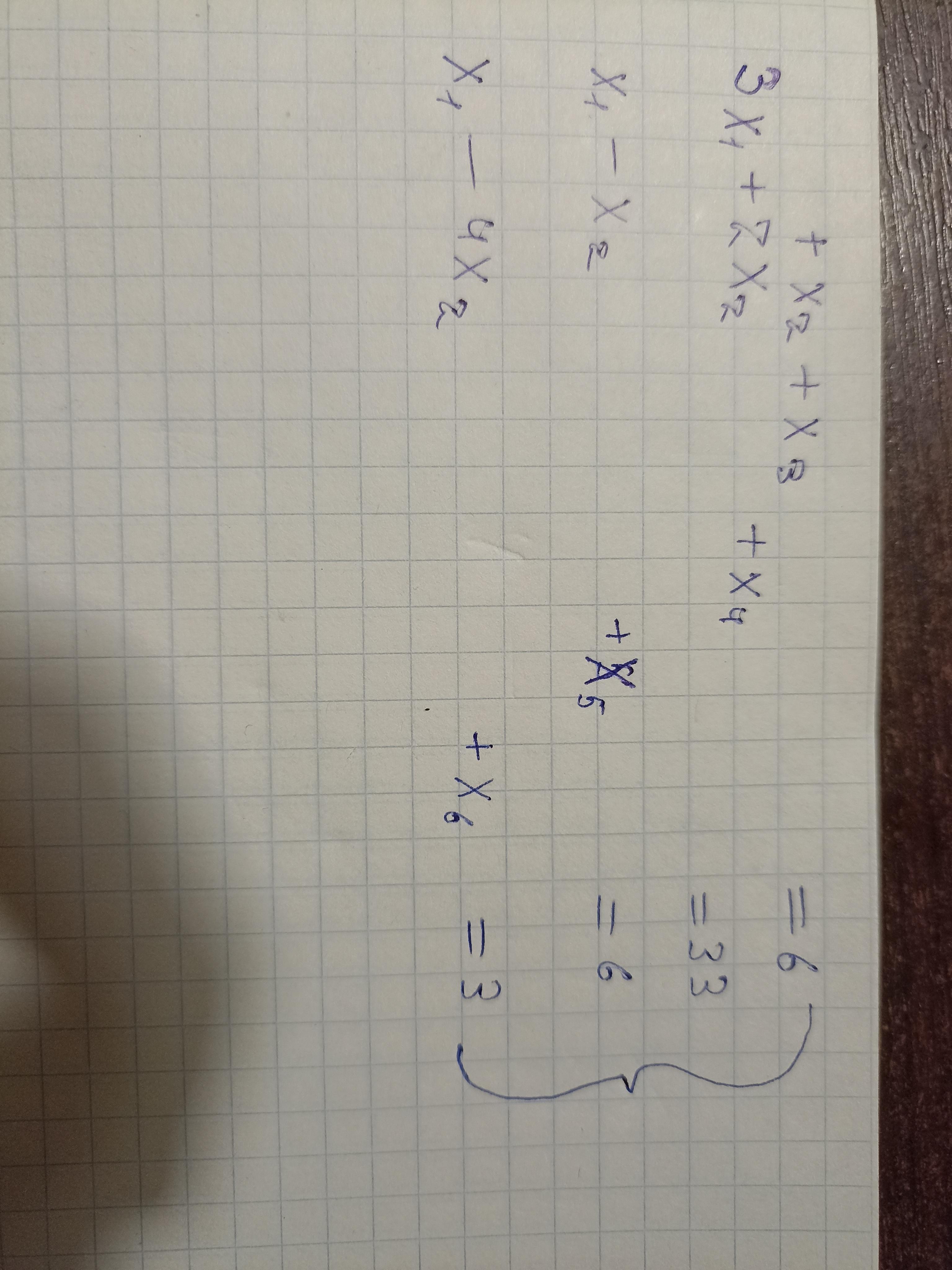
Ответы
Ответ:
Решить систему линейных уравнений .
Приведём расширенную матрицу системы к ступенчатому виду .
Сначала 3 строку поставили 1 место .
Затем 1 стр. умножим на (-3) и сложим с 3 стр. ;
1 стр. умножим на (-1) и сложим с 4 стр.
2 стр. умн. на (-5) + 3 стр. ; 2 стр. умн. на 3 + 4 стр.
3 cтр. умн. на 3 + 4 стр. , умноженная на 5
Получили систему из 4 уравнений с 6 неизвестными . Ранг матрицы системы равен рангу расширенной матрицы , r = 4 . Значит система совместна . Так как n=6 < r=4 , то система имеет бесчисленное множество решений .
Выбираем базисные неизвестные . Это будут х₁ , х₂ , х₃ , х₄ , так как определитель, составленный из первых 4-х столбцов отличен от 0 и равен -15 ≠ 0 . Свободными неизвестными будут х₅ , х₆ .
Пусть свободные неизвестные принимают значения
. Тогда решение системы запишем в виде :


