Предмет: Алгебра,
автор: gorgdompl
Довести...в файлі
допоможіть
Приложения:
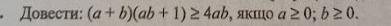
Ответы
Автор ответа:
0
Ответ:
Объяснение:
формула:
Похожие вопросы
Предмет: Русский язык,
автор: uliapolubok39
Предмет: Химия,
автор: ladunec08
Предмет: Математика,
автор: Glebmarkin
Предмет: История,
автор: alesiaartemkina
Предмет: Химия,
автор: Dgureeryy