ОЧЕНЬ СРОЧНО 50 БАЛЛОВ
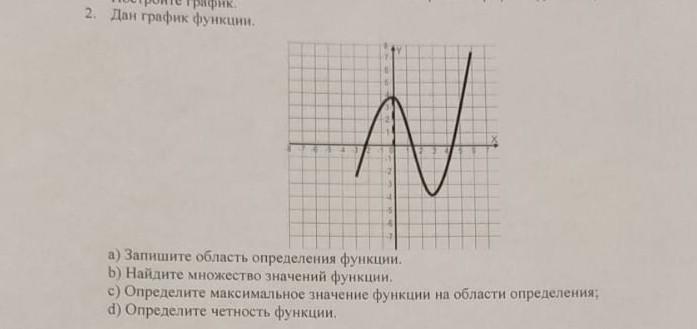
2. Дан график функции. N а) Запишите область определения функции. b) Найдите множество значений функции. с) Определите максимальное значение функции на области определения: d) Определите четность функции.
Ответы
Ответ:a) D(y) = [-6; 6]
b) Е(у) - [-3; 7]
c) у > 0 при х ∈ [-6; -4) ∪ (1; 6]; y < 0 при х ∈ (-4; 1)
d) y наиб. = у (-6) = 7
e) данная функция не является четной или нечетной, то есть, общего вида
f) Возрастает на промежутке: [-2; 4];
Убывает на промежутках: [-6; -4], [4; 6].
Объяснение:a) Запишите область определения функции.
b) Найдите множество значений функции.
c) Определите промежутки знакопостоянства функции;
d) Определите максимальное значение функции на области определения;
е) Определите четность функции.
f) Определите интервалы возрастания и убывания функции.
a) Запишите область определения функции.
- все допустимые значения аргумента (х).
D(y) = [-6; 6]
b) Найдите множество значений функции.
- все значения функции (у) на области определения.
Е(у) - [-3; 7]
c) Определите промежутки знакопостоянства функции.
1) Выше оси Ох:
у > 0 при х ∈ [-6; -4) ∪ (1; 6]
2) Ниже оси Ох:
y < 0 при х ∈ (-4; 1)
d) Определите максимальное значение функции на области определения.
y наиб. = у (-6) = 7
е) Определите четность функции.
Четная функция симметрична оси Оу, нечетная функция симметрична началу координат.
У нас ни то, ни другое.
⇒ данная функция не является четной или нечетной, то есть, общего вида.
f) Определите интервалы возрастания и убывания функции.
Функция возрастает, если при увеличении аргумента (х), значение функции (у) тоже увеличивается.
Возрастает на промежутке: [-2; 4]
Функция убывает, если при увеличении аргумента (х), значение функции (у) уменьшается.
Убывает на промежутках: [-6; -4], [4; 6]