Предмет: Алгебра,
автор: Sofiasst
ОЧЕНЬ СРОЧНО!!!!Нужно сделать все задания!!! Даю 50 балов
Приложения:

Ответы
Автор ответа:
0
Ответ:
1) Выражение в знаменателе дроби не может равняться 0 .
2) При каком значении переменной дробь равно 0 ?
3) Сократить дробь .
4) Сократить дробь . Применяем формулу разности квадратов .
Приложения:

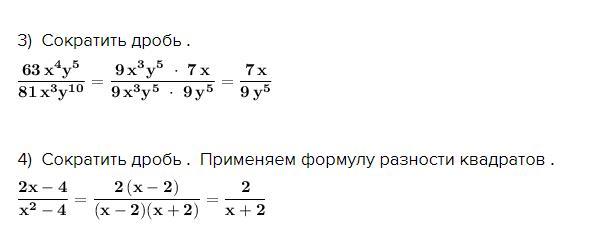
Похожие вопросы
Предмет: Математика,
автор: reytskayaalina
Предмет: Химия,
автор: Мади
Предмет: Українська мова,
автор: kiriswqr008777
Предмет: Алгебра,
автор: дондондери
Предмет: Математика,
автор: kingsmagic2017