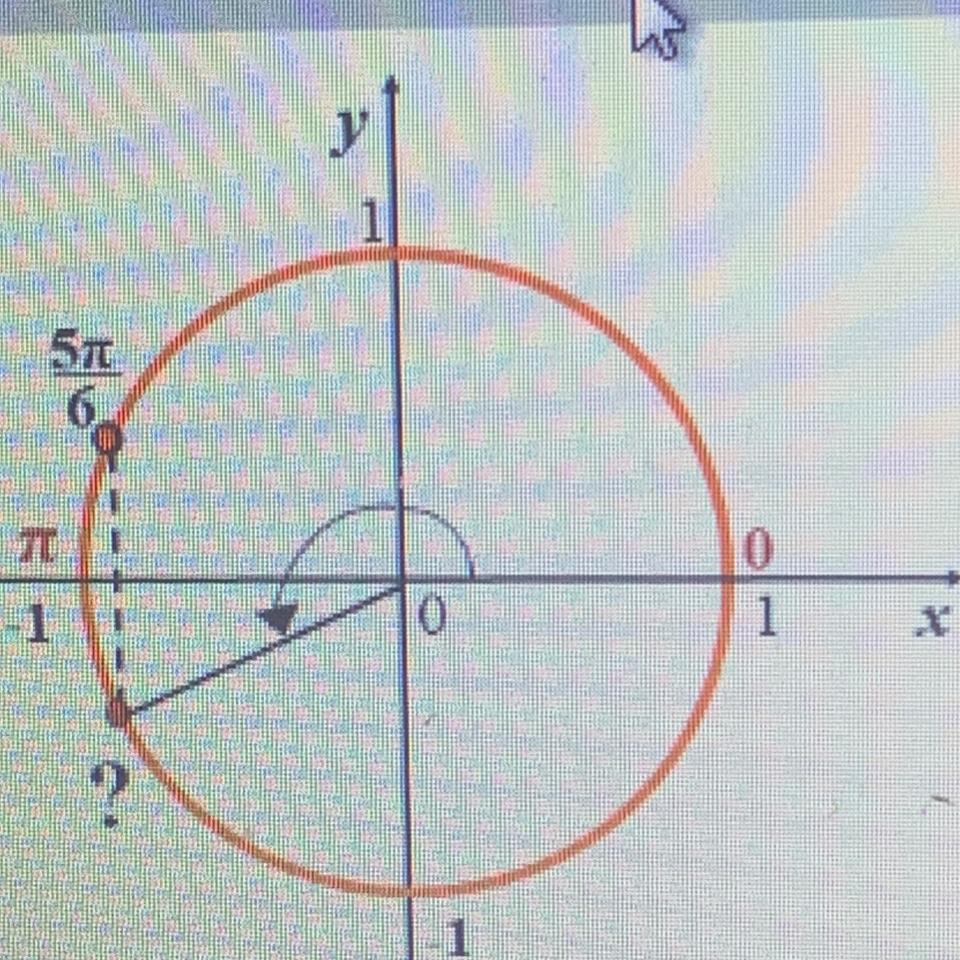
знайдіть кут
а) п/6
б)4п/6
в)7п/6
Ответы
Для знаходження значень тригонометричних функцій кутів, нам потрібно знати їхній величини у виразі в радіанах. В даному випадку, ви надали значення кутів у вигляді десяткових дробів множини числа π (пі) (наприклад, π/6).
Давайте знайдемо значення косинуса та синуса для кожного з них:
а) Кут π/6:
cos(π/6) = √3/2
sin(π/6) = 1/2
б) Кут 4π/6 (або просто 2π, оскільки 4π/6 = 2π):
cos(2π) = 1
sin(2π) = 0
в) Кут 7π/6:
cos(7π/6) = -√3/2
sin(7π/6) = -1/2
Отже, значення косинуса та синуса для кожного з цих кутів в радіанах виглядають так:
а) cos(π/6) = √3/2, sin(π/6) = 1/2
б) cos(2π) = 1, sin(2π) = 0
в) cos(7π/6) = -√3/2, sin(7π/6) = -1/2
Це - значення косинуса та синуса цих кутів. Якщо вам потрібно знайти значення тангенсу, це можна зробити, поділивши значення синуса на значення косинуса:
а) tan(π/6) = (1/2) / (√3/2) = 1/√3
б) tan(2π) = 0 / 1 = 0
в) tan(7π/6) = (-1/2) / (-√3/2) = 1/√3
Надіюся, це допомагає вам знайти косинус, синус і тангенс кожного з наведених кутів.