Предмет: Алгебра,
автор: saminkamalink
№58 ПОЛНОСТЬЮ СРОЧНО!ДАМ 35 БАЛЛОВ
Приложения:
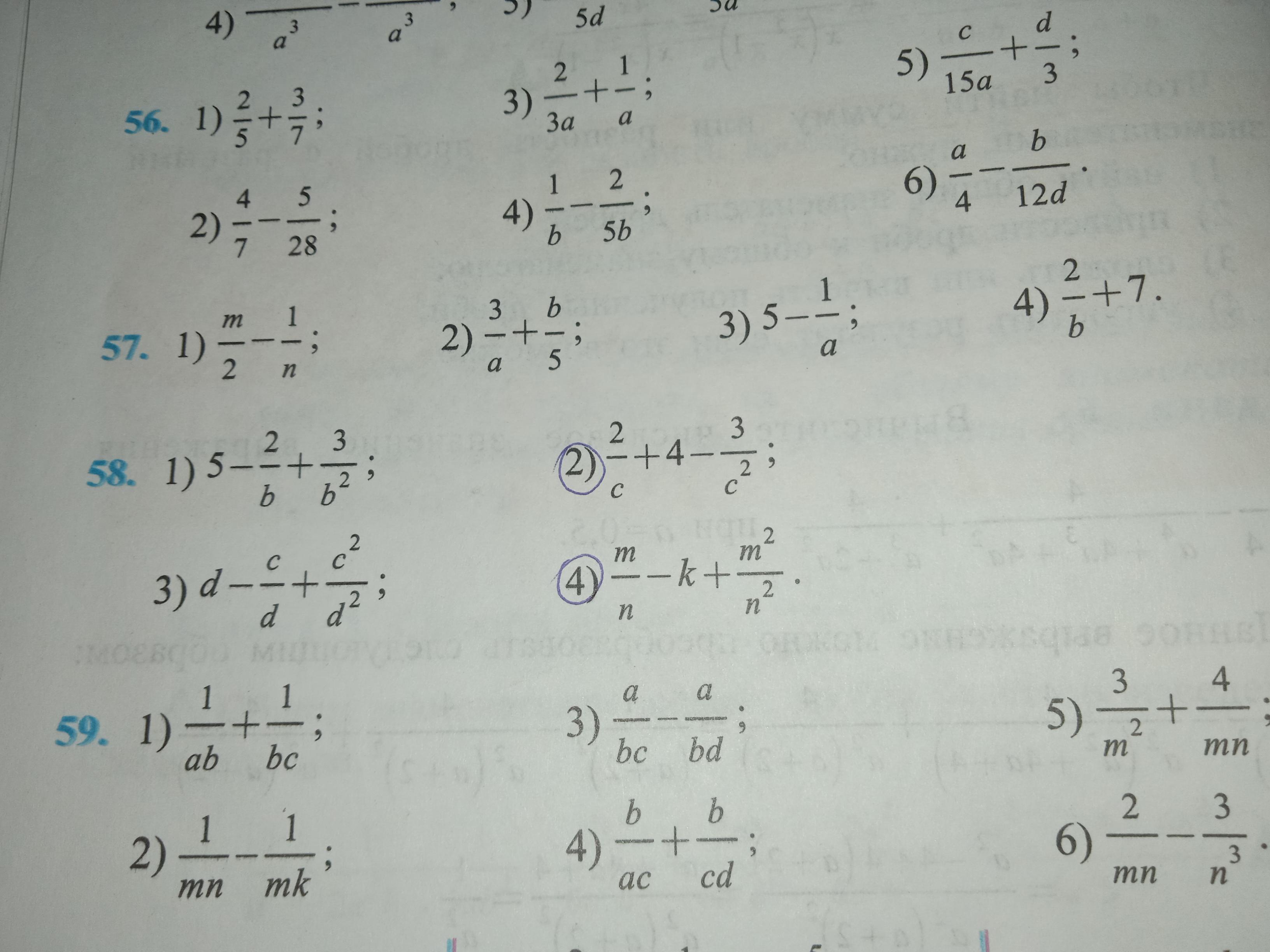
Ответы
Автор ответа:
1
Ответ:
Начнем с общего знаменателя. Нам нужно найти наименьшее общее кратное для знаменателей c и c^2, которыми являются c^2. Поэтому приведем оба члена к общему знаменателю c^2:
(2c^2/c^2) + (4c^2/c^2) - (3/c^2)
Теперь объединим числители в один:
(2c^2 + 4c^2 - 3) / c^2
Сложим числители:
(6c^2 - 3) / c^2
Таким образом, упрощенное выражение равно (6c^2 - 3) / c^2.
saminkamalink:
мне не в кружке нужно было...а полностью...но всё равно спасибо
Для начала объединим первые два члена:
5 - 2/b = (5b - 2) / b
Теперь у нас есть:
(5b - 2) / b + 3/b^2
Чтобы сложить эти две дроби, нужно привести их к общему знаменателю. Общим знаменателем будет b^2. Поэтому приведем первую дробь к знаменателю b^2, умножив и числитель, и знаменатель на b:
(5b - 2) / b + 3/b^2 = (5b^2 - 2b) / (b^2) + 3/b^2
Теперь, когда у нас есть общий знаменатель, мы можем сложить дроби:
(5b^2 - 2b + 3) / b^2
Итак, упрощенное выражение равно:
(5b^2 - 2b + 3) / b^2
5 - 2/b = (5b - 2) / b
Теперь у нас есть:
(5b - 2) / b + 3/b^2
Чтобы сложить эти две дроби, нужно привести их к общему знаменателю. Общим знаменателем будет b^2. Поэтому приведем первую дробь к знаменателю b^2, умножив и числитель, и знаменатель на b:
(5b - 2) / b + 3/b^2 = (5b^2 - 2b) / (b^2) + 3/b^2
Теперь, когда у нас есть общий знаменатель, мы можем сложить дроби:
(5b^2 - 2b + 3) / b^2
Итак, упрощенное выражение равно:
(5b^2 - 2b + 3) / b^2
Выражение: (d - c) / (d + c^2/d^2)
Сначала преобразуем дробь в знаменателе:
d + c^2/d^2 = d + (c^2/d^2)
Теперь, когда у нас есть общий знаменатель, мы можем объединить дроби:
(d - c) / (d + c^2/d^2) = (d - c) / (d + c^2/d^2)
Для упрощения этой дроби, давайте умножим числитель и знаменатель на d^2, чтобы избавиться от дроби в знаменателе:
(d - c) / (d + c^2/d^2) * (d^2/d^2) = (d^3 - cd^2) / (d^3 + c^2)
Таким образом, упрощенное выражение равно:
(d^3 - cd^2) / (d^3 + c^2)
Сначала преобразуем дробь в знаменателе:
d + c^2/d^2 = d + (c^2/d^2)
Теперь, когда у нас есть общий знаменатель, мы можем объединить дроби:
(d - c) / (d + c^2/d^2) = (d - c) / (d + c^2/d^2)
Для упрощения этой дроби, давайте умножим числитель и знаменатель на d^2, чтобы избавиться от дроби в знаменателе:
(d - c) / (d + c^2/d^2) * (d^2/d^2) = (d^3 - cd^2) / (d^3 + c^2)
Таким образом, упрощенное выражение равно:
(d^3 - cd^2) / (d^3 + c^2)
Выражение: (m/n) - k + (m^2/n^2)
Для начала объединим первые два члена:
(m/n) - k = (m - kn) / n
Теперь у нас есть:
(m - kn) / n + (m^2/n^2)
Чтобы сложить эти два члена, нужно привести их к общему знаменателю. Общим знаменателем будет n^2. Приведем первую дробь к знаменателю n^2, умножив и числитель, и знаменатель на n:
(m - kn) / n + (m^2/n^2) = (m^2 - kn^2) / n^2 + (m^2/n^2)
Теперь, когда у нас есть общий знаменатель, мы можем сложить дроби:
(m^2 - kn^2 + m^2) / n^2
2m^2 - kn^2
2m^2 - kn^2 / n^2
Для начала объединим первые два члена:
(m/n) - k = (m - kn) / n
Теперь у нас есть:
(m - kn) / n + (m^2/n^2)
Чтобы сложить эти два члена, нужно привести их к общему знаменателю. Общим знаменателем будет n^2. Приведем первую дробь к знаменателю n^2, умножив и числитель, и знаменатель на n:
(m - kn) / n + (m^2/n^2) = (m^2 - kn^2) / n^2 + (m^2/n^2)
Теперь, когда у нас есть общий знаменатель, мы можем сложить дроби:
(m^2 - kn^2 + m^2) / n^2
2m^2 - kn^2
2m^2 - kn^2 / n^2
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Английский язык,
автор: erasylproshka
Предмет: Русский язык,
автор: akjolahmetbek3
Предмет: Математика,
автор: alleksiiaa
Предмет: Українська мова,
автор: ivanchukvadim77