Question

Основа прямого паралелепіпеда - прямокутник зі стороною 8 см та діагоналлю 17 см. Висота призми - 3/46 см. Тоді площа бічної поверхні призми дорівнює:

Answer 1

Ответ:

Площа бічної поверхні призми дорівнює 3 см²

Объяснение:

Основа прямого паралелепіпеда - прямокутник зі стороною 8 см та діагоналлю 17 см. Висота призми - 3/46 см. Тоді площа бічної поверхні призми дорівнює:

• Паралелепипед, бічні ребра якого перпендикулярні до площин основи, називають прямим паралелепіпедом.

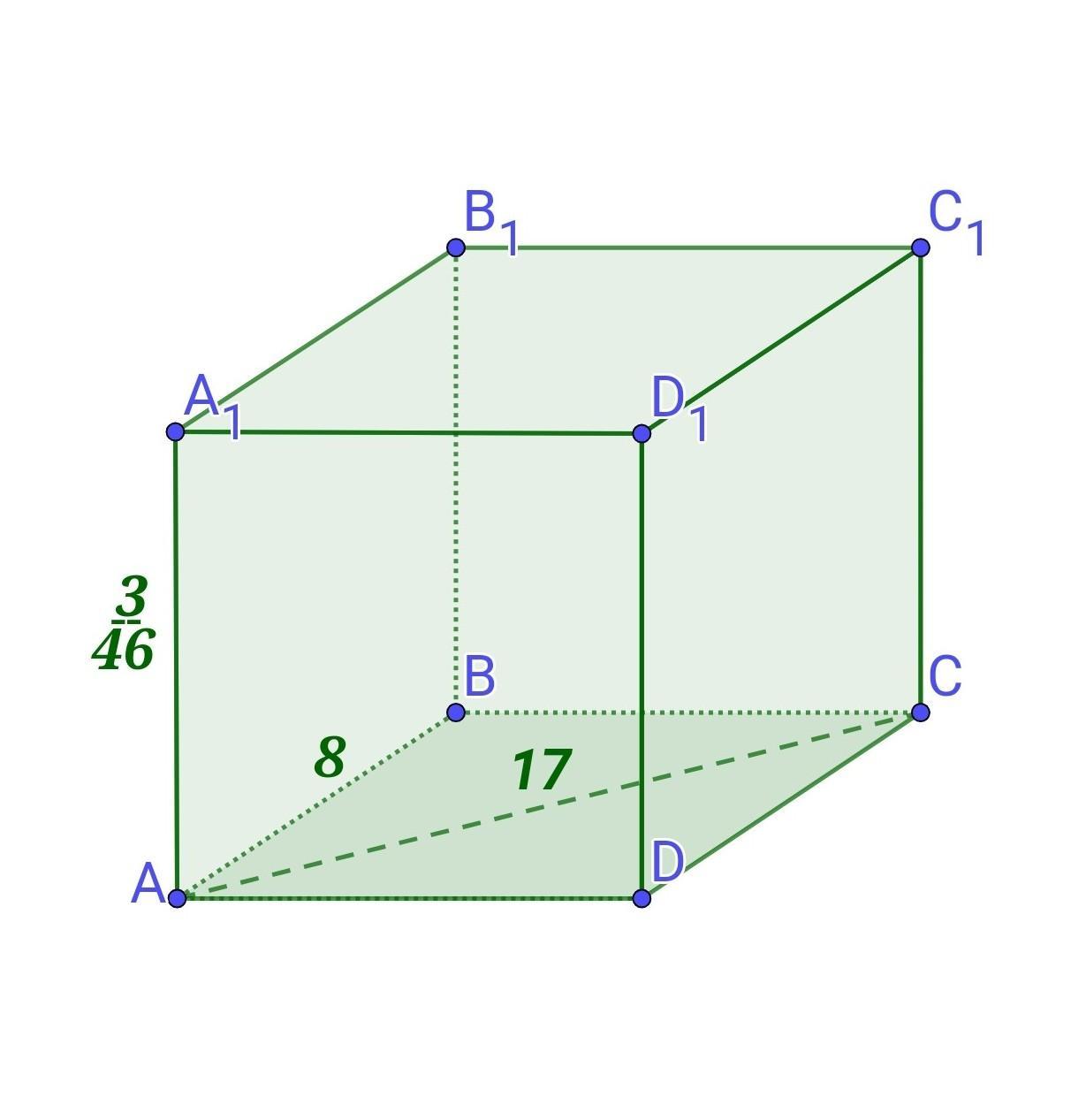
Нехай ABCDA₁B₁C₁D₁ - прямий паралелепіпед, ABCD - прямокутник, AB = 8 см, АС = 17 см, висота паралелепіпеда АА₁ = 3/46 см.

Площа бічної поверхні призми знайдемо за формулою:

Sб. = Росн. • Н

де Н = АА₁ - висота призми.

Периметр основи (прямокутника): Росн. = 2 • (АВ + ВС)

ВС знайдемо з прямокутного трикутника ABC (∠В=90°) за теоремою Піфагора:

ВС² = АС² - АВ² = 17² - 8² = 289 - 64 = 225

ВС = 15 см

Росн. = 2 • (8 + 15) = 2 • 23 = 46 (см)

$S = 46\cdot \dfrac{3}{46} = \bf 3$ (см²)

#SPJ1