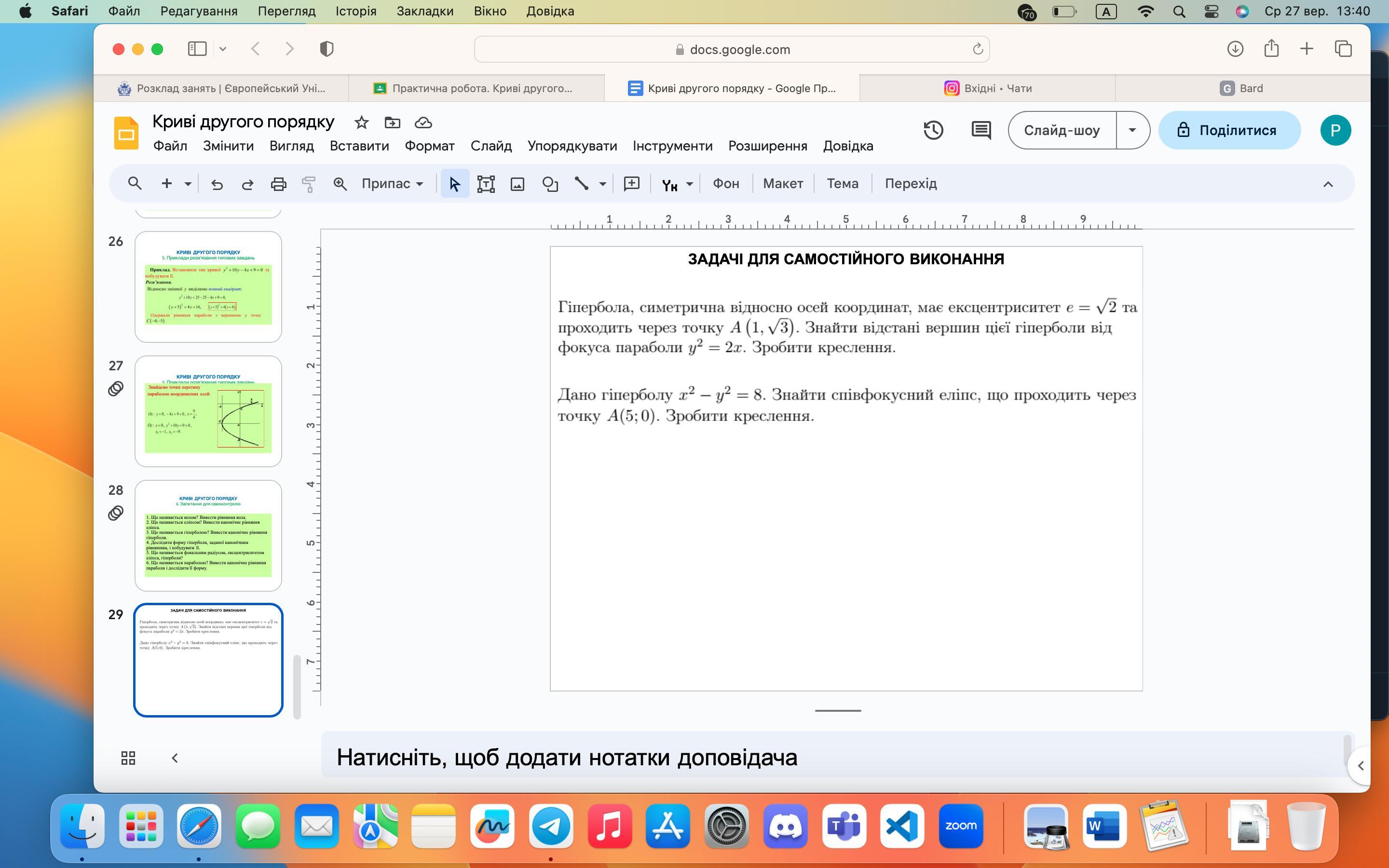
Аналітична геометрія. Виконати ці 2 завдання і накреслити
Ответы
1) Эксцентриситет равносторонней гиперболы равен √2.
Это гипербола с равными полуосями.
Её уравнение x² - y² = a² при условии, что действительная ось по оси Ох.
Подставим координаты точки А: 1² - (√3)² = 1 – 3 = -2.
Так как отрицательное число не может быть квадратом, то это признак того, что действительная ось направлена по оси Оу.
Тогда её уравнение будет -x² + y² = a².
Подставим координаты точки А: -1² + (√3)² = a².
-1 + 3 =a².
Отсюда a² = 2, а = √2.
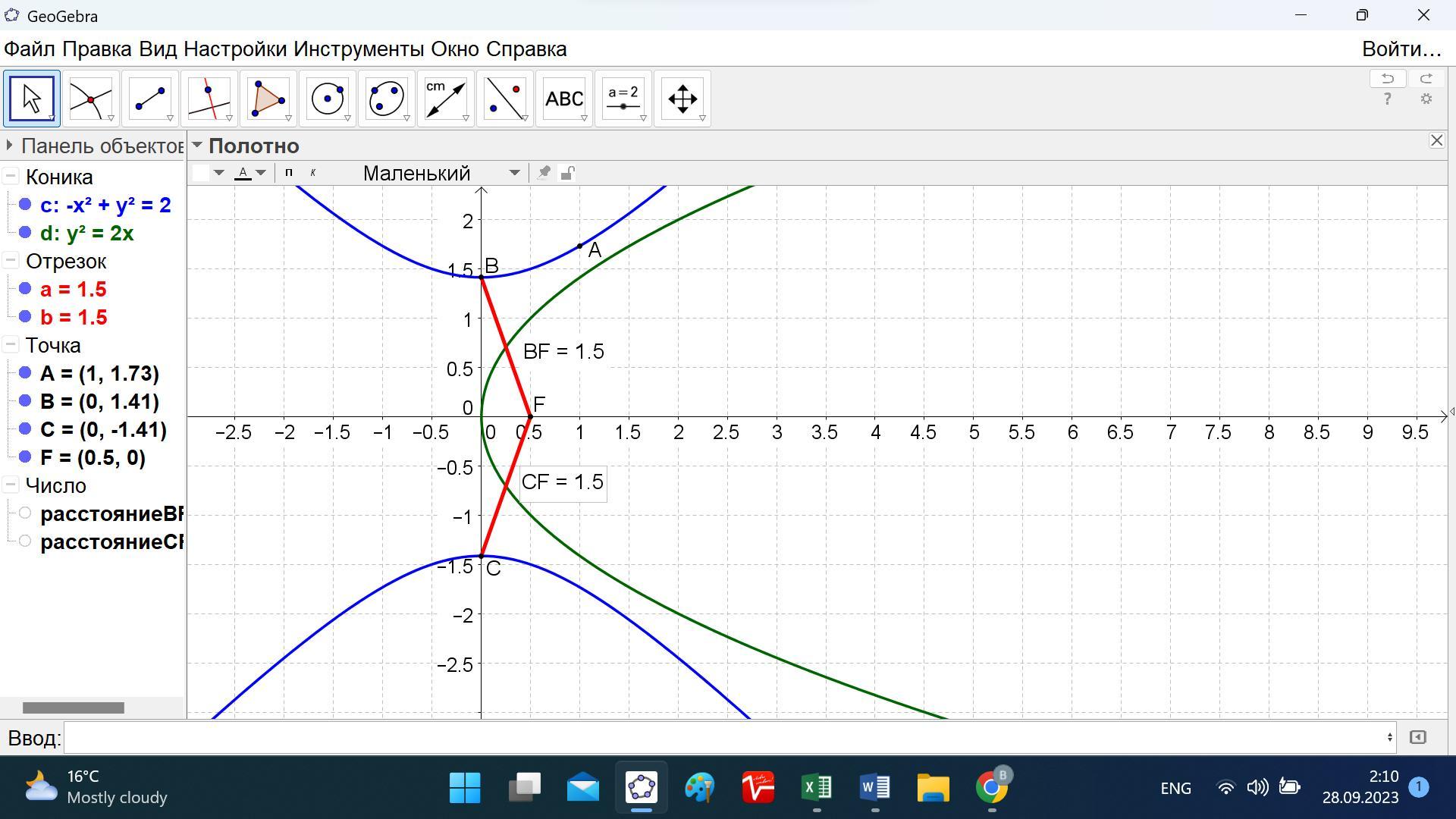
Уравнение заданной гиперболы -x² + y² =(√2)².
Получаем координаты вершин гиперболы В(0; √2) и С(0; -√2).
Теперь переходим к параболе.
Уравнение параболы в канонической системе координат имеет вид: y² = 2px, где p - расстояние от фокуса до директрисы параболы.
Заданное уравнение y² = 2x приведём к каноническому y² = 2*1x.
Отсюда получаем расстояние от вершины до фокуса, равное р/2 = ½.
Координаты фокуса F(0,5; 0).
Находим решение как расстояние между точкой F и точками В и С.
FВ = √((0-0,5)² + (√2-0)²) = √(0,25 + 2) = √2,25 = 1,5.
FС = √((0-0,5)² + (-√2-0)²) = √(0,25 + 2) = √2,25 = 1,5.
2) Дана гипербола x² - y² = 8.
Приведём уравнение к каноническому, разделив обе части на 8.
Получаем (x²/8) – (y²/8) = 1.
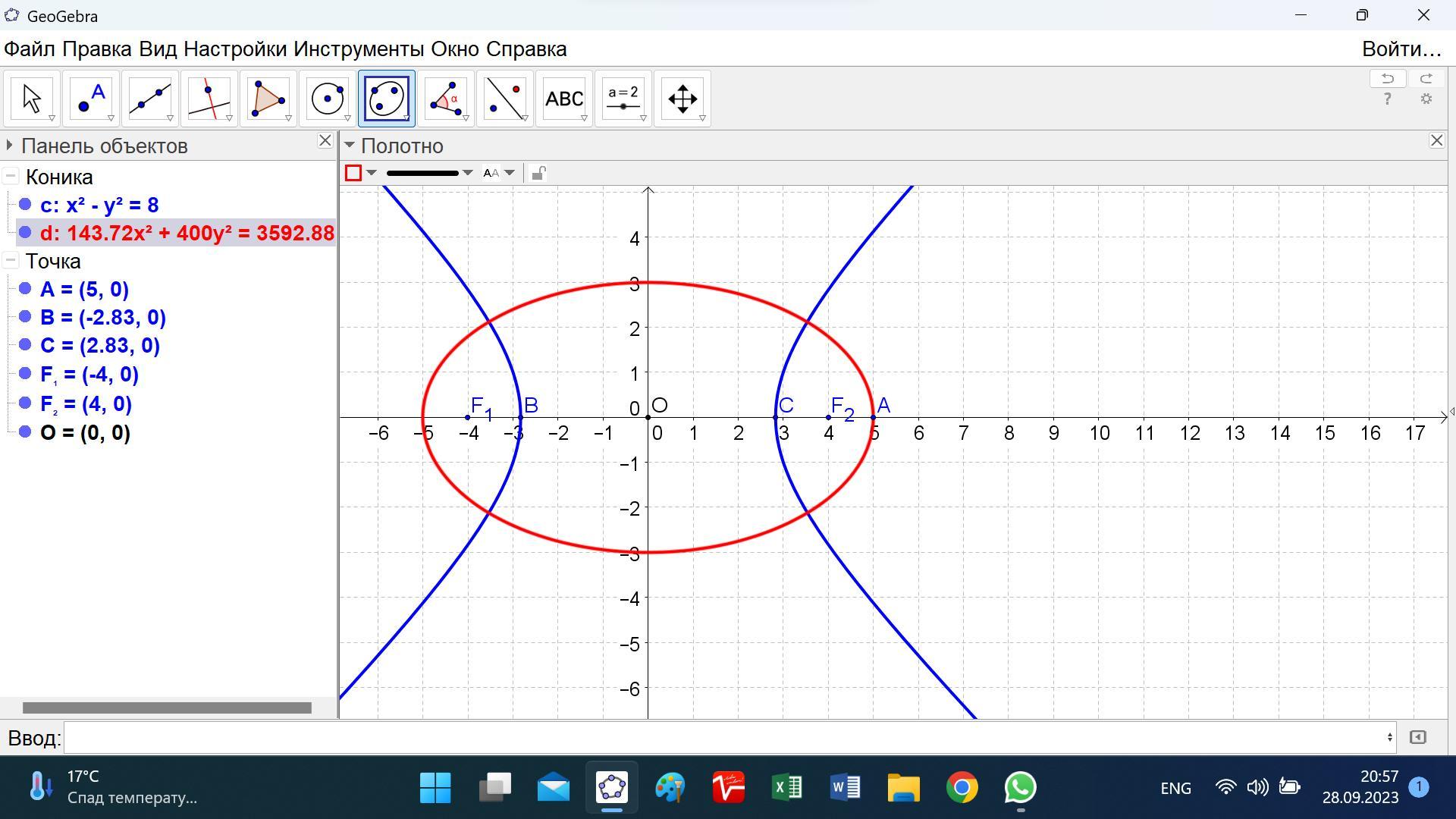
Это равносторонняя гипербола с осями a = b = √8 = 2√2 с центром в начале координат. Эксцентриситет такой гиперболы равен √2.
Фокусы её находятся в точках F1, F2 = +-(√8*√2) = +-4.
Теперь переходим к эллипсу с фокусами именно в этих же точках, проходящую через точку А(5; 0).
Уравнение эллипса: (x²/a²) + y²/b²) = 1.
Так как фокусы эллипса в точках +-4, то расстояние от каждого из фокусов до начала координат равно с = 4.
Координаты точки А(5; 0) говорят о том, что это одна из вершин эллипса, а именно в положительном направлении оси Ох. Значит, большая ось а = 5.
Расстояние от каждого из фокусов до начала координат равно:
c = √(a² - b²). Отсюда находим значение b:
b = √(a² - c²) = √(5² - 4²) = √(25 - 16) = √9 = 3.
Получаем уравнение эллипса (x²/5²) + y²/3²) = 1.